Capacitance

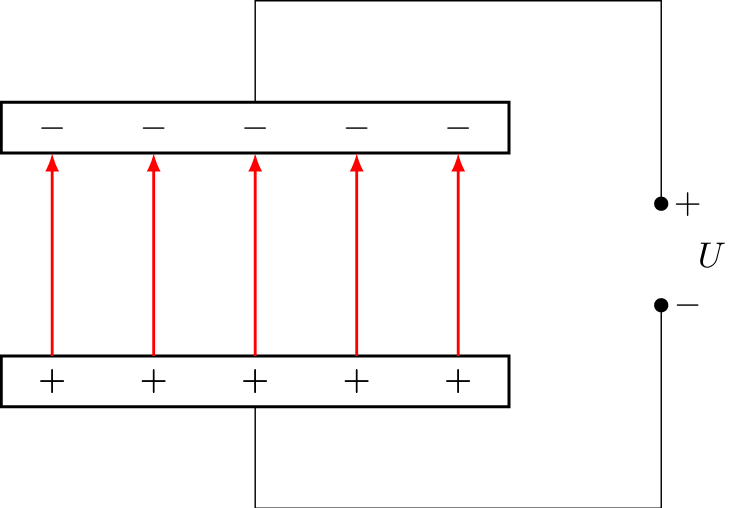
A capacitor is an electrical device that can store charge and energy. The easiest setup contains simply two parallel plates at which a voltage is applied. Such a device is called a parallel-plate capacitor. The figure below shows two parallel plates with a small distance connected to a voltage source, e.g. a battery. The positive pole sucks and draws away some of the electrons from the plates, whereas the negative pole brings some electrons to the surface of the plates. The more charge can be stored at a given voltage, the higher the capacitance. Although it is possible to use units like $C/V$ to describe the capacitance, it is considered to be very important and therefore gets its own unit called Farad (F). This unit is named after Michael Faraday who was a pioneer in the investigation of electrostatic and electrodynamic phenomena. Typical values of commonly used capacitors in electrical devices are given in Nanofarad (nF) or Microfarad (μF). Very special capacitors called supercapacitors or ultracapacitors can have a capacitance up to a few Farad. However, they are usually quite expensive and very sensitive to electrostatic discharges. We want to calculate now the capacitance of such a capacitor analytically. We assume that these plates occupy an infinitely large area so that any effects on the borders can be omitted. In this case, the charge is evenly distributed throughout the surfaces, i.e. we can simply define a surface density as the charge per unit area: $$\sigma = \frac{Q}{A}$$ With the help of the electric fux, the following equation can be written down: $$EA = \frac{Q}{\varepsilon_0} = \frac{\sigma A}{\varepsilon_0}$$ Cancelling out the area $A$ on both sides, results in the electric field for two large plates: $$\boxed{E = \frac{\sigma}{\varepsilon_0}}$$ Now we can insert everything into the formula of the capacitance which leads to $$C = \frac{Q}{U} = \frac{\sigma A}{U}$$ and then with $\sigma = E/\varepsilon_0$ to $$C = \frac{E\varepsilon_0 A}{U}$$ Now the relation $E=U/d$ with $d$ being the plate distance is used to cancel out $U$. The final result is then given as $$\boxed{C = \varepsilon_0\frac{A}{d}}$$ This formula can be used to calculate the capacitance of any plate capacitor. Typical capacitors for electronic devices contain very long and thin metal foils which are rolled up and packed into tiny packages. They are therefore called film capacitors. Since a real capacitor has a finite plate size, the effects on the edges cannot be ignored anymore as shown in the following figure. In this plot, the right plate is charged positively and the left one contains a negative charge. In order to study their influence on capacitance, numerical simulations have to be performed, because analytical calculations would be too difficult. In the next step, we want to calculate the energy that is stored inside the electric field of a capacitor after charging it up with a power supply. For this purpose, we assume that we bring a small amount $\mathrm{d}Q$ of charge from the outside to the surfaces of the capacitor plates. With every charge, the required work and therefore the stored energy increases according to $$\mathrm{d}W = \mathrm{d}E = U\mathrm{d}Q$$ We can now replace $U$ with the help of the formula $U = Q/C$ which leads to $$\mathrm{d}E = \frac{Q}{C}\mathrm{d}Q$$ Integrating overall charges $$E = \int_{0}^{Q} \frac{Q}{C}\mathrm{d}Q$$ results in the following formula for the energy: $$\boxed{E = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}CU^2}$$ For the right side of the equation, $Q$ was replaced with $CU$, in order to find a relation between the energy and the voltage. The strong relation between the voltage and the stored energy is sometimes used in flashlights of photo cameras. After transforming the small voltage of the included batteries up to around $500\,\mathrm{V}$, it is then used to charge up huge capacitors. The capacitor is quickly being discharged which leads to the emission of visible light within a very short period of time. The resulting power is therefore much higher than a small battery can deliver. The same method is usually used for defibrillators. A smaller voltage is first transformed to a higher one and then charges up a capacitor. The stored energy is located within 100 and 200 Joules and can be used to create shock pulses with a higher power.