Effective Values

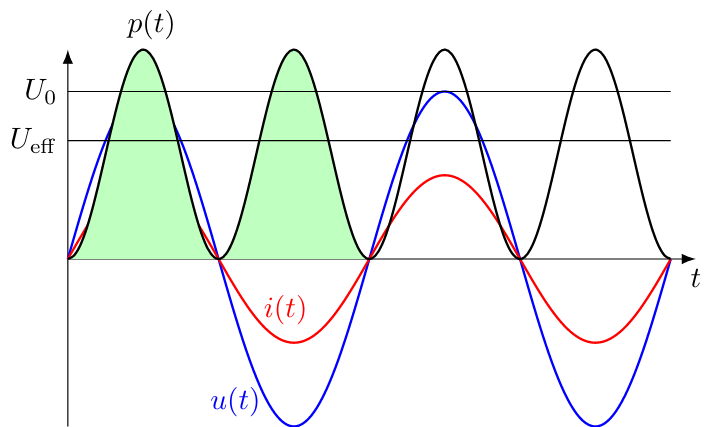
We have seen already that for a DC voltage, the power output is simply the product of the voltage and the current $P = UI$. In the case of an AC voltage, on the other hand, $U$ and $I$ cannot simply be replaced by the peak values $U_0$ and $I_0$, since both voltage and current fluctuate around the zero line. As a result, the product of the time-dependent current $I(t)$ and voltage $U(t)$, which is namely the power $P(t) = U(t)I(t)$, oscillates with respect to time. However, the power can never become negative, since the signs of $U(t)$ and $I(t)$ are always both positive or negative. We want to find now a mean value for the power that corresponds to the heat dissipation of a DC voltage. Mathematically, this average can be achieved using the time integral over the power, i.e. over the product of current and voltage. The result then has to be divided by the period $T$: $$\bar{P} = \frac{1}{T}\int_0^TU(t)I(t)\,\mathrm{d} t = \frac{1}{T}\int_0^T U_0I_0\sin^2(\omega t)\,\mathrm{d} t$$ Since the current and voltage at an ohmic resistor do not show any phase difference, the product of both quantities is always positive. In order to be able to easily calculate this integral, the following trigonometric transformation is carried out: $$\sin^2(x) = \frac{1}{2}(1-\cos 2x)$$ If one integrates this function and then insert the corresponding limits $0$ and $T$, the following relationship can be calculated: $$\bar{P} = \frac{1}{2}U_0I_0 = \frac{U_0}{\sqrt{2}}\frac{I_0}{\sqrt{2}}$$ In the last step, the factor 1/2 was divided into the product of current and voltage. It makes sense to give these two fractions their own names and formula letters. With the effective values of the AC voltage, it is, therefore, possible to calculate the power that a DC voltage with these voltage values and currents generates as heat at an ohmic resistor.