Electric Current
Table of Contents
Definition
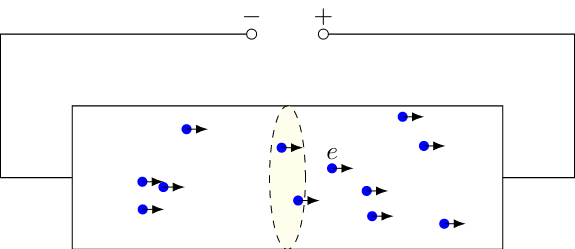
Electric Current Definition
Here, $Q$ is the full amount of charge, i.e. all electrons moving inside the wire. Since the current in a wire is created by moving electrons, this formula can be rewritten as
$$I = \frac{ne}{t}$$
for a constant current. Here, $n$ stands for the number of electrons and $e$ for the elementary charge.
The electric current is defined as the amount of charge that travels through the cross-section of the wire per unit of time. We can write this in the following form: $$I = \frac{\mathrm{d}Q}{\mathrm{d}t}$$
Current Density
Current Density Definition
Although this quantity is called density, it is important to remember that it refers to the amount of charge per area and not per volume. The current density can therefore be written as
$$j = \frac{\mathrm{d}I}{\mathrm{d}A}$$
Substituting $I$ with $\mathrm{d}Q/\mathrm{d}t$ gives
$$j = \frac{\mathrm{d}^2Q}{\mathrm{d}A\,\mathrm{d}t}$$
In the next step, we replace $\mathrm{d}Q$ with the product $\varrho \mathrm{d}V$ where $\varrho$ is the charge density that is assumed to be constant. This leads to the following expression of the charge density:
$$j = \varrho \frac{\mathrm{d}V}{\mathrm{d}t\,\mathrm{d}A}$$
We can now rewrite $\mathrm{d}V/\mathrm{d}A$ with $\mathrm{d}s$:
$$j = \frac{\mathrm{d}s}{\mathrm{d}t}$$
Replacing $\mathrm{d}s/\mathrm{d}t$ with the speed $v$ of the charge finally results in
$$j = \varrho v$$
This is a very important formula to compute the current density if the density and speed of the charges are known. We can of course rewrite this statement in vector form to generalize it further.
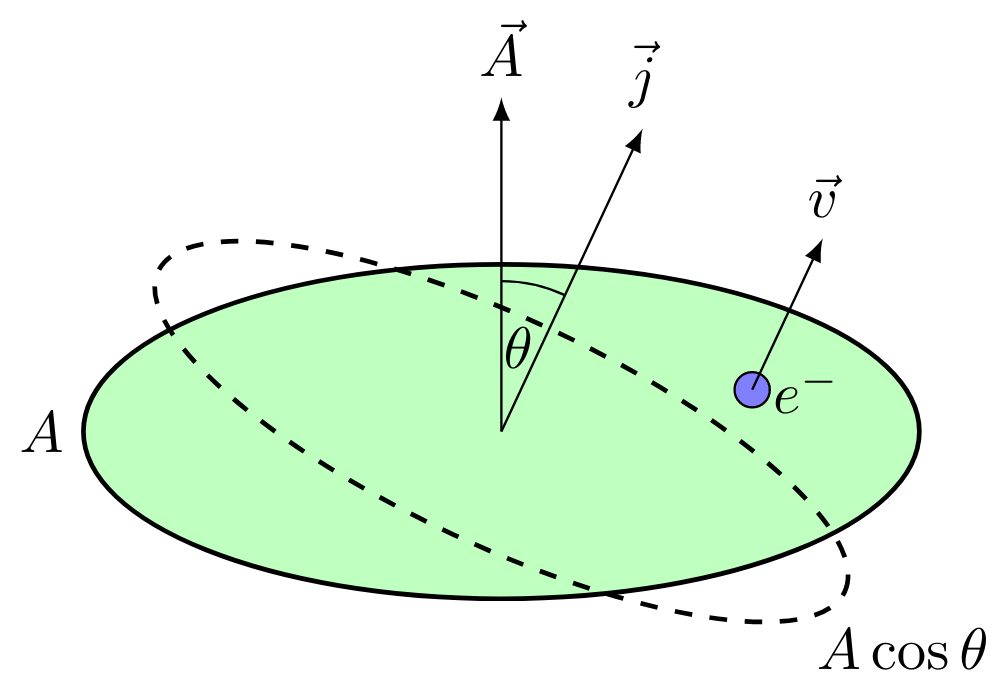
The electric current equals the integral over the charge density $\vec{j}$ multiplied with the area vector $\vec{A}$: $$I = \int \vec{j}\cdot \mathrm{d}\vec{A}$$
Current Density and Velocity
The current density $\vec{j}$ can be calculated with the product of the moving charge density $\varrho$ and its velocity $\vec{v}$: $$\vec{j} = \varrho \vec{v}$$
This page contains 626 words and 3707 characters.
Last modified: 2022-10-01 18:37:09 by mustafa