Electric Field

• The electric field is defined as the fraction of the resulting force per charge $$\vec{E} = \frac{\vec{F}}{q}$$
• The smallest in nature appearing charge is the elementary charge with the value $$e = 1.602176634\cdot 10^{-19}\,\mathrm{C}$$

Although we experience different kinds of forces in our daily life, we can break them down into two different types of interactions. The first one is gravitation which acts between all bodies that have a mass. The second one is the electric force which affects all objects with an electric charge. Both forces have in common that they are distance forces, i.e. they act via space between bodies that are far away from each other. In contrast to that, we also know contact forces which only act between bodies touching each other. However, these contact forces do not exist in nature. All forces we observe are direct consequences of the electric force.

This can be understood with the help of the following example. If you put a pen on the desk, it does not fall through the table, although the gravitation pulls on it. The reason for this observation can be seen in the fact that electrons inside the atomic structure of the pen interact via the electric force with the electrons inside the table. Due to equal charges, they repel each other. This example also shows that the electric force is by many orders of magnitude larger than the gravitation because it even prevents heavy objects to fall to the center of the earth. The reason, why we only feel gravitation in our daily life is because masses do only attract each other, whereas the electrons in an atom neutralize the electric field of protons which makes atoms neutral. Another result of electric forces is friction which mainly occurs because atoms of one body interact with atoms of another body.

Since all forces are results of action at a distance, physicists have developed the idea of an electric field that surrounds electric charges. This field has an infinite range and could be in principle even observed several lightyears away from the charge itself. Michael Faraday has mainly worked on the idea to define a source charge surrounded by that electric field. 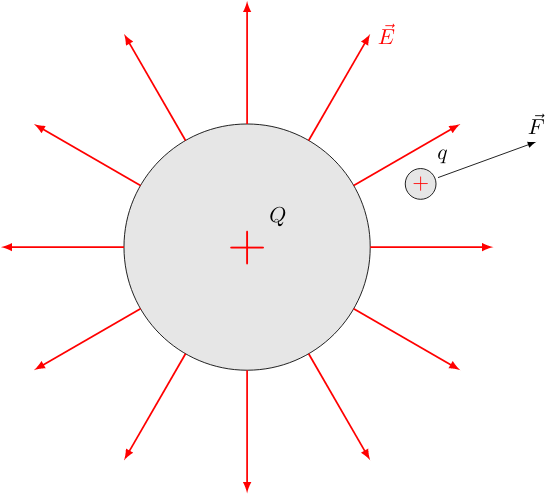If then another charge, the so-called test charge, gets into that field, it feels a force acting on it which is either attracting or repelling, depending on the type of the charge. The situation of positive source and test charges is shown in the figure below. Due to the existence of the electric field $\vec{E}$ of the source charge $Q$, a force $\vec{F}$ acts on the test charge $q$. Usually, the source charge is labeled with a capital $Q$ and the test charge with a small $q$. The unit of the electric charge is Coulomb (C). There are two types of charges existing: positive $+q$ and negative $-q$ ones. Opposite charges attract each other, whereas equal charges repel each other. The smallest in nature occurring charge is the elementary charge which is often denoted with $e$. The existence and quantitative value of this charge can be measured for example with the help of the Millikan Experiment.

This value equals the charge of an electron with a negative value $q=-e$ and a proton with a positive value $q=+e$. Due to this reason, they completely compensate for each other and atoms are neutral. Neutrons, which are also part of the atomic nucleus, are not charged and therefore do not create an electric field. From the above-mentioned facts, we can now derive a definition of the electric field and its value.

This formula is of course only valid as long as the charge is small enough, not to disturb the field. However, it is very important to keep in mind, that we only take a look at the field of the source, not the one of the test charge. Furthermore, the electric field of the source does always exist, even if no test charge is present. The unit of the electric field is $N/C$ which simply follows from its definition $F/q$. Later we will also come to know about other units that can be used for the electric field, but of course, they can always be derived from that form. 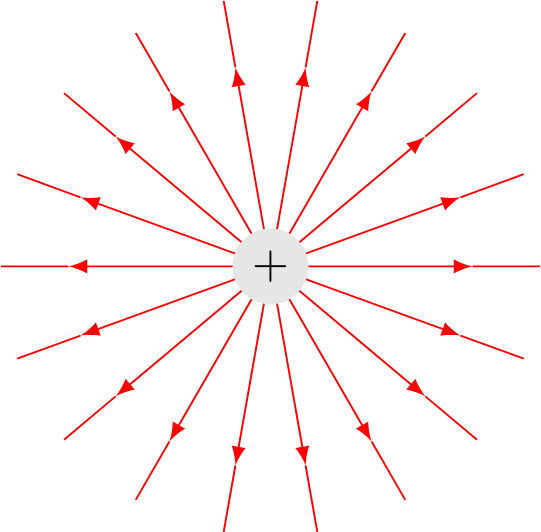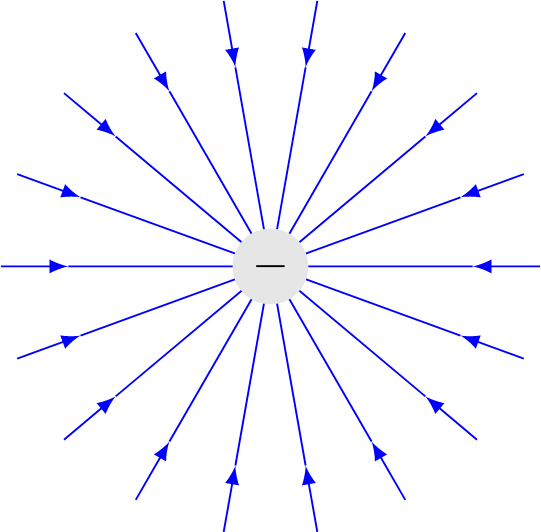Electric fields can be visualized with the help of field lines. The direction of the field lines is defined to point from the positive charge to the negative one. In the following figures, you can see the electric field lines of point charges with $q > 0$ and respectively for $q < 0$. At each point, a vector can be drawn tangential to the field lines. Field lines are furthermore not allowed to overlap. The strength of the electric field is given by the density of the field lines. A higher amount of field lines in a given volume results in a higher electric field.

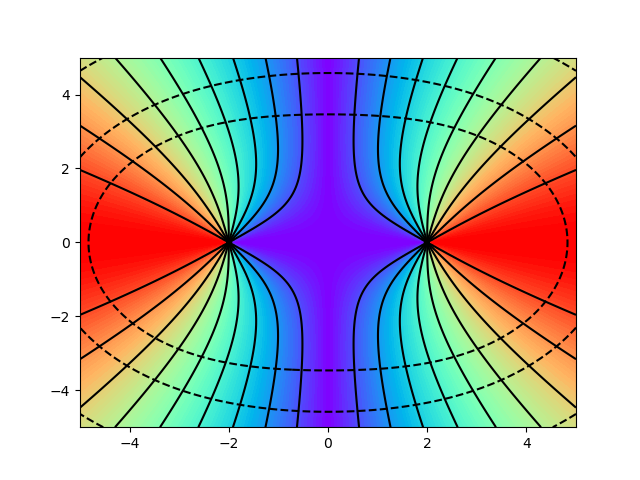
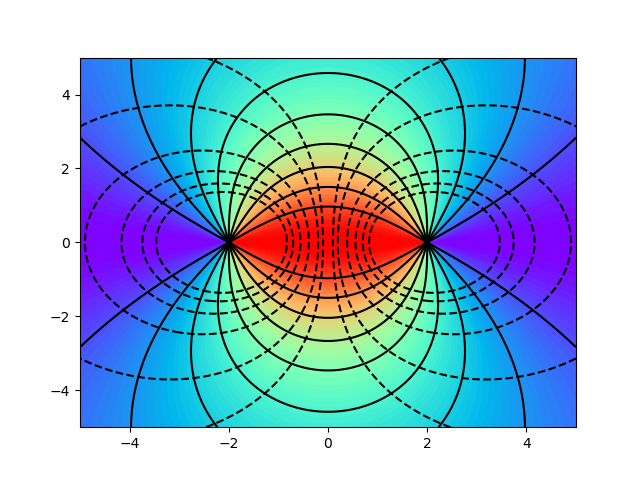
The following figures show the field lines of two charges at positions -2 and +2 with opposite and equal signs using solid lines and colored faces. The equipotential areas are illustrated with dashed lines.

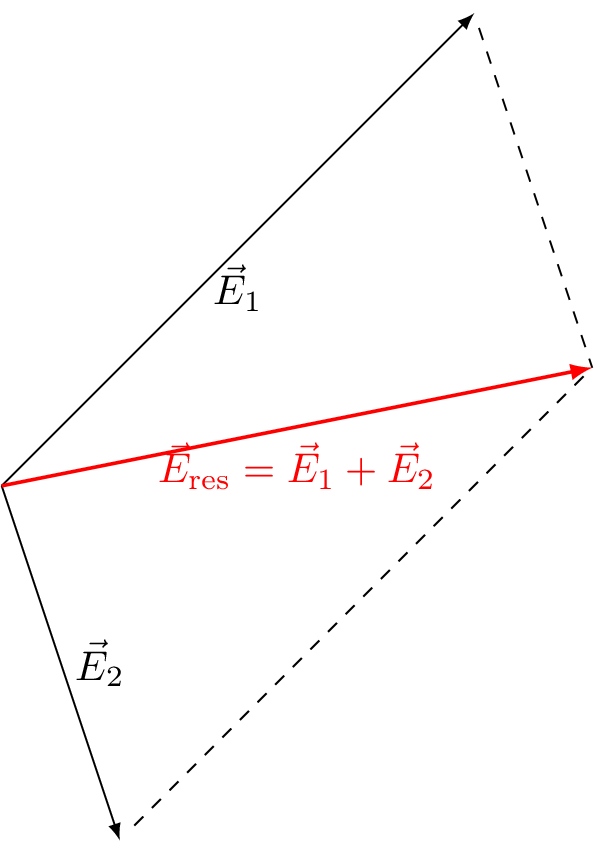
The equipotential areas are always perpendicular to the field lines. If a charge is moved along one of these areas, no work is done. Every charge creates an electric field. Electric fields have a direction and absolute value and are therefore described with the help of vectors. In the presence of multiple charges, all electric fields have to be added up vectorially in each point. This can be seen in the following figure with two vectors $\vec{E}_1$ and $\vec{E}_2$ adding up to a resulting vector $\vec{E}_\mathrm{res}$ at a given point. If a charge is located inside an electric field, the applied force leads to acceleration along the field lines. Assuming a homogenous field, that is also constant in time, we can calculate the acceleration according to the 2nd law of Newton: $$\vec{a} = \frac{\vec{F}}{m} = \frac{q\vec{E}}{m}$$ where $m$ is the mass of the charge. The mass of an electron for instance has been experimentally determined to $$m_e = 9.1093837015\,\mathrm{kg}$$ Old oscilloscopes with cathode ray tubes contained large plates forming a nearly homogenous electric field in either $x$- order $y$-direction. After accelerating the electrons inside a high electric field with several kilovolts, they were distracted by the electric field of these plates according to the shape of the measured signal. When they hit the screen in front, their path can be followed by the observer with the help of a shining fluorescence layer.