Electric Flux
Integral Form
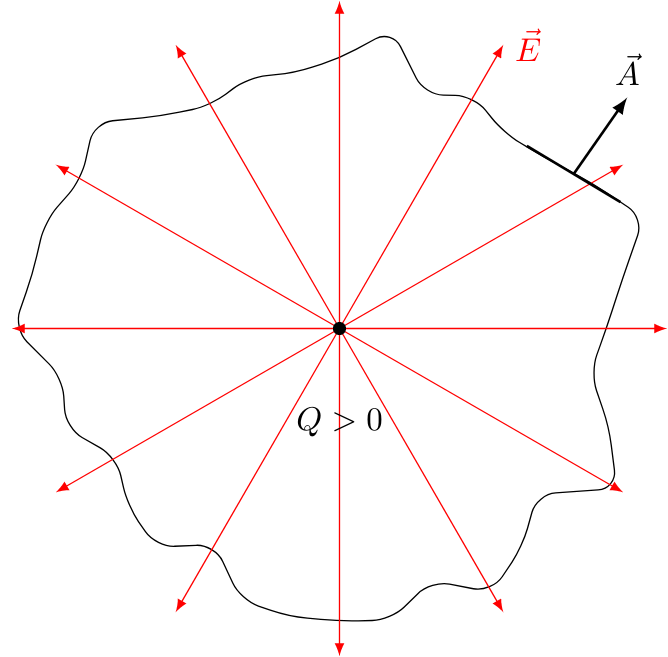
Every area integral of a vector quantity is called "flux". After defining the properties of the electric field $\vec{E}$, we want to take a look at the definition of the electric flux $\Psi$ as the integral over the dot product of the electric field and the area vector of any arbitrary surface.
Electric Flux
The electric flux of the electric field $\vec{E}$ and the area $\vec{A}$ is defined as
$$\Psi = \oint \vec{E}\cdot\mathrm{d}\vec{A}$$
We can imagine this integral as the number of field lines passing a particular area. In order to understand this concept a bit better, we can take a look at a point charge placed inside an arbitrary volume.
It can be shown experimentally that the electric flux is proportional to the charge inside the closed surface. This is also called
Gauss' law of Electrostatics. Because it contains an integral, it is more precisely called the
Integral Form of Gauss' Law:
Gauss' Law of Electrostatics (Integral Form)
The total electric flux is through a given surface is proportional to the charge covered by that surface with the proportional constant as being the inverse electric field constant:
$${\oint \vec{E}\cdot\mathrm{d}\vec{A} = \frac{Q}{\varepsilon_0}}$$
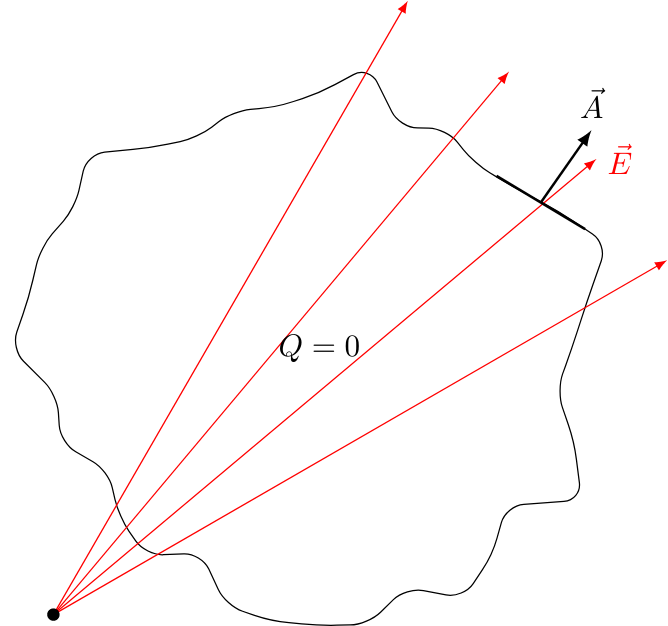
If we now draw the charge outside of this volume, all electric field lines pass the surface of this volume. Therefore, the electric flux is 0.
Example For the case of a charged sphere, all field lines are exactly perpendicular to an arbitrarily chosen sphere around it. Therefore, the left side of the equation can be written as
$$\oint \vec{E}\cdot\mathrm{d}\vec{A} = EA = E4\pi r^2 = \frac{Q}{\varepsilon_0}$$
where $A=4\pi r^2$ is the area of the sphere at a distance $r$ from the center of the charge. Solving the equation for $E$ results in
$$E = \frac{Q}{4\pi\varepsilon_0 r^2}$$
Now, the force acting on another charge is given as
$$F = qE = \frac{qQ}{4\pi\varepsilon_0 r^2}$$
which is exactly matching with Coulomb's law.
Differential Form
We can use Gauss' law to show that for every surface it can be written
$$\Psi = \oint \vec{E}\cdot\mathrm{d}\vec{A} = \int \mathrm{div}\vec{E}\,\mathrm{d}V$$
On the other hand, we can turn the charge into an integral of the the charge density:
$$\Psi = \frac{1}{\varepsilon_0}Q = \frac{1}{\varepsilon_0}\int\varrho\,\mathrm{d}V$$
Equating both fluxes leads to
$$\int \mathrm{div}\vec{E}\,\mathrm{d}V = \frac{1}{\varepsilon_0}\int\varrho\,\mathrm{d}V$$
Since the integration happens over the same volume, the integral vanishes and the following important statement appears which is also called the
Differential Form of Gauss' Law.
Gauss' Law of Electrostatics (Differential Form)
The divergence of the electric field is directly proportional to the charge density
$${\mathrm{div}\vec{E} = \frac{\varrho}{\varepsilon_0}}$$
It states that distributed charges in space are sources for $\varrho > 0$ or sinks in case of $\varrho < 0$ of the electrical flux.
This page contains 656 words and 3898 characters.
Last modified: 2022-10-01 18:36:32 by mustafa
Electric flux for a point charge inside an arbitrary volume.
Electric flux for a charge outside of a given boundary.
