Hall Effect

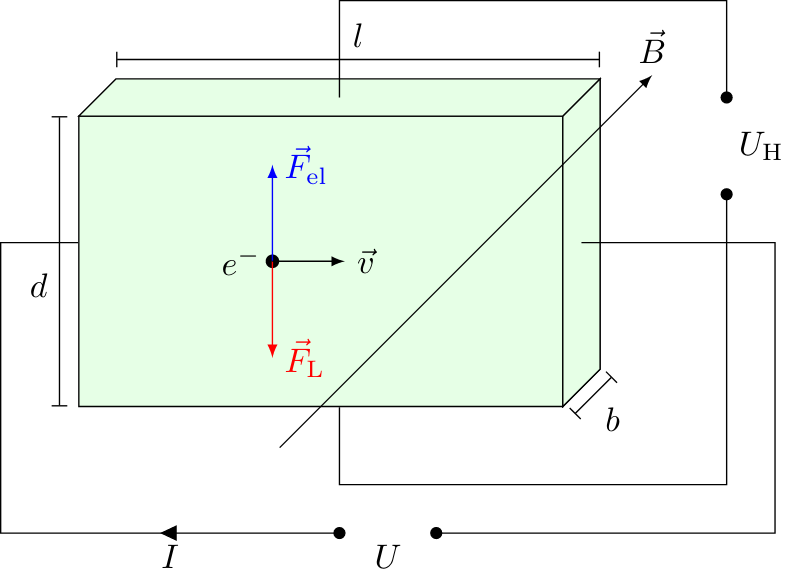
The hall effect is related to the Lorentz force acting on electrons inside a wire. It was named after the American physicist Edwin Hall and is used to measure the strength of magnetic fields. The strength of magnetic fields is usually measured with calibrated Hall probes, whereby the measuring principle is based on the Hall effect. The following figure illustrates this principle with the help of a conductor placed inside a magnetic field with the strength $B$. The magnetic field lines are parallel to the side $b$. By applying a voltage $U$ to both sides of the conductor, a current $I$ flows through it parallel to the length $l$ and perpendicular to the $B$-field. The electrons are then deflected perpendicular to the field lines and the direction of movement as a direct result of the Lorentz force $F_\mathrm{L}$. The deflection continues until the electric force $F_\mathrm{el}$ has completely compensated for the Lorentz force, due to the electrically repulsive field $\vec{E}$ between all charges $Q$. In this case, the following condition is fulfilled: $$F_\mathrm{el} = F_\mathrm{L}$$ If you insert the corresponding formulas, you get: $$QE = QvB$$ We now assume that the part of the conductor inside the magnetic field has length $l$. With $v=l/t$ and $I=q/t$ we get: $$QE = IBl$$ This formula we had already seen when deriving the Lorentz force from the force acting on a conductor. The total charge $Q$ can be calculated from the electron density $n$ (electrons per cubic meter) and the volume $V$ of the conductor as follows: $$Q = nVe = ndlbe$$ The thickness of the conductor was denoted with $d$ and its width with $b$. Therefore, in the last step, the volume $V$ was replaced with the product of all sides $d$, $b$, and $l$. If you insert this relationship and the relationship $E=U/d$ into the equation above, then you get a formula for the Hall voltage. The Hall voltage increases with a larger current and magnetic flux density but it is inversely proportional to the electron density and the thickness of the conductor in the direction of the magnetic field lines. For this reason, semiconductors with fewer free electrons are usually more suitable than highly conductive metals. And in addition, the sensitive material has to be very thin, in order to decrease the value of $b$. Nevertheless, the achievable Hall voltages are usually so small that they have to be additionally amplified with voltage amplifiers in order to deliver an adequate signal. Some textbooks do not directly give an overview of the electron density $n$ but instead define a material-dependent Hall constant as follows. In this case, the formula for Hall voltage can be written down as follows: $$\boxed{U_\mathrm{H} = A_\mathrm{H}\frac{IB}{d}}$$ The sign of the Hall constant depends on whether the current is predominantly caused by electrons, as in metal, or by holes, as in semiconductors. The Hall constants are usually difficult to determine and scatter very widely. Tiny impurities and temperature fluctuations have a very large impact on the measured value.