Kirchhoff's Circuit Laws

When electric wires meet at a point, that point is called a node. Just as the volume flow of an incompressible liquid must always be constant in a closed pipe system (Hagen-Poiseuille), the current strength in an electric circuit cannot change. From that, it follows that the sum of all incoming currents must be equal to the sum of outgoing currents and the node remains neutral. This is the formulation of the nodal rule, which is also called first Kirchhoff's law and is mathematically defined for $n$ inflowing and outflowing currents as follows. 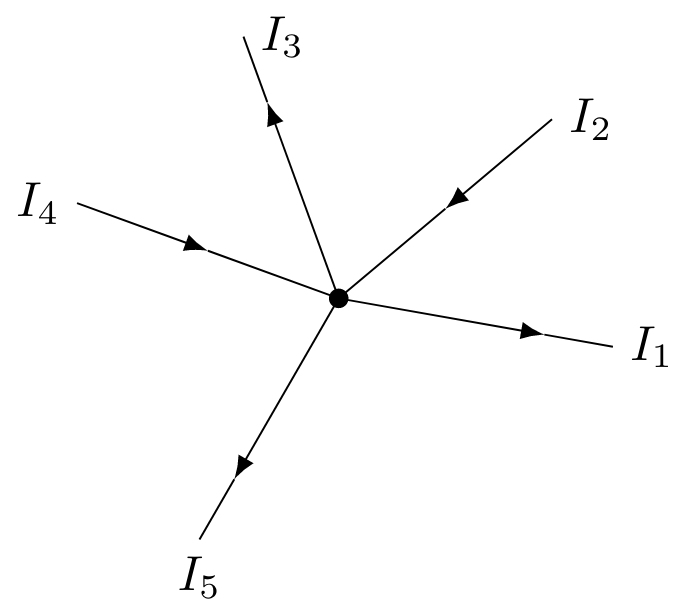For reasons of convention, incoming currents are given a positive value and outgoing currents are given a negative sign. As an example, we take a look at 5 currents as shown in the figure below. Here, $I_2$ and $I_4$ are outgoing currents, whereas $I_1$, $I_3$ and $I_5$ flow into the node. Using the nodal rule, we obtain: $$-I_1 + I_2 - I_3 + I_4 - I_5 = 0$$ Of course, all signs can also be reversed without changing the value of the sum. In addition to the current, the energy in a circuit must also be conserved. Since the energy is directly linked to the electrical voltage, the partial voltages of a circuit in a mesh must always add up to 0, i.e. for $n$ resistances in a mesh, the following must apply the following second rule of Kirchhoff. 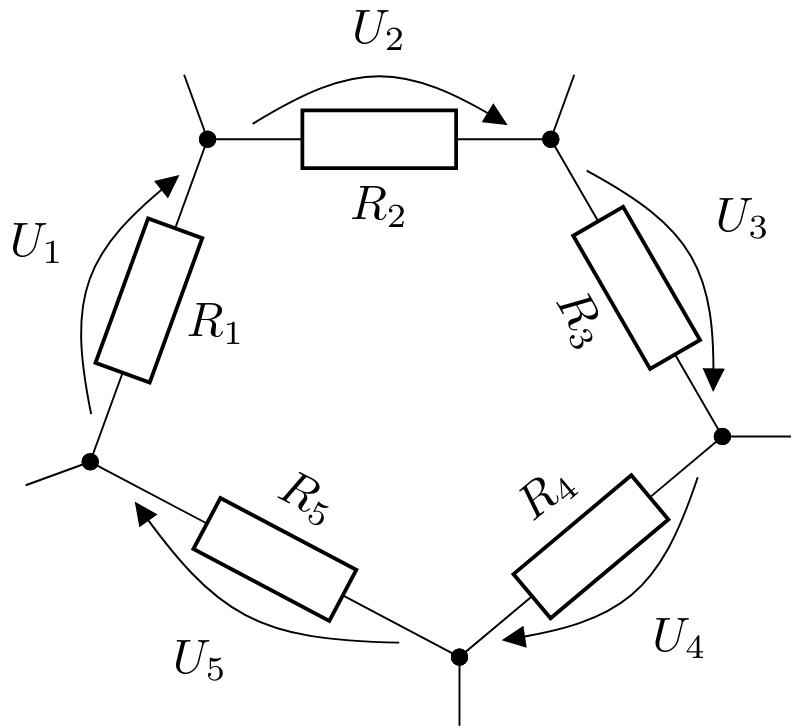The signs result from the direction of flow of the current, analogous to the node rule. The direction of rotation can be chosen arbitrarily, but the signs must be adjusted accordingly if the direction is reversed. As an example, we take a look at a circuit with 5 meshes as shown in the following figure. Since the current in this mesh flows in the same direction everywhere, the sum of the partial voltages is: $$U_1 + U_2 + U_3 + U_4 + U_5 = 0$$ However, when the voltage is used, care must always be taken to select the correct sign. If there is a voltage source in the mesh, either the source voltage or the individual voltages must be given a minus sign.