Lorentz Force

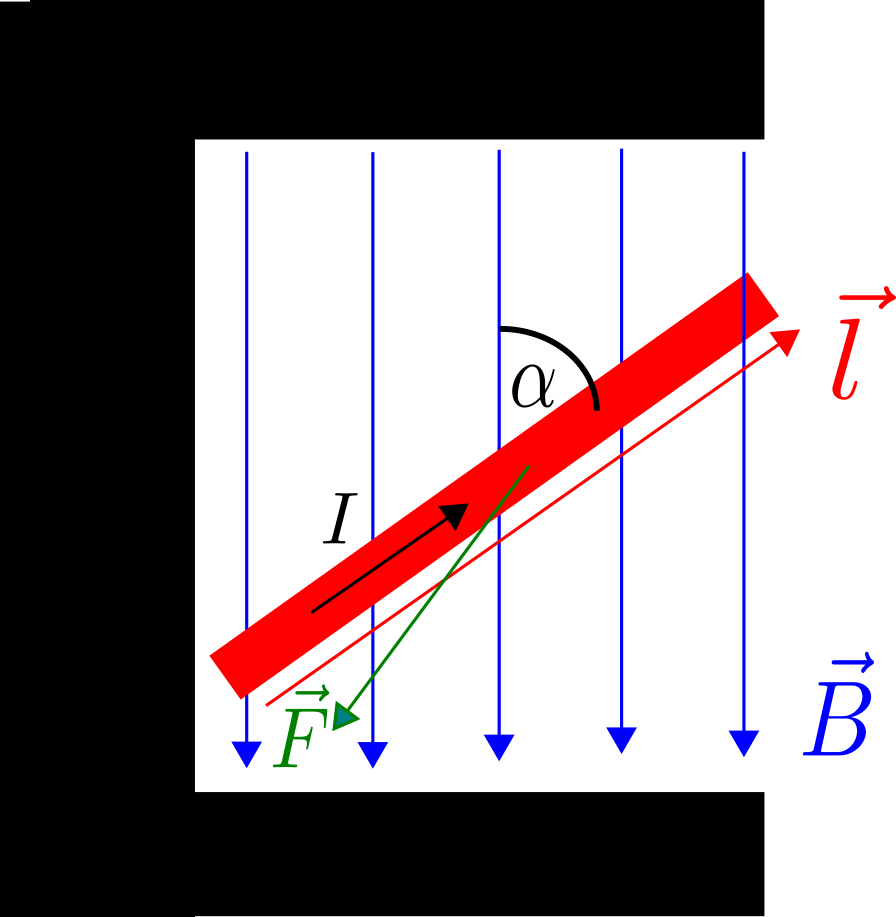
Let us imagine a current $I$ flowing through a conductor with the length $l$. If we place the conducting wire inside a magnetic field with the strength $B$ and field lines perpendicular to the wire, then a force acting on the conductor can be observed. Experimentally it was found that this force is proportional to $I$, $l$, and $B$ which can be written in the following form $$\boxed{F_\perp = IlB}$$ If the orientation of the wire is not perpendicular to the field lines, the force gets smaller by a factor of $\sin\varphi$ where $\varphi$ is the angle between the wire and the field lines: $$F = IlB\sin\varphi$$ This formula can be taken as the absolute value of the following cross product: $$\vec{F} = I\vec{l}\times\vec{B}$$ where the vector $\vec{l}$ represents the length and direction of the wire. The force acts therefore perpendicular to the direction of the wire and the magnetic field lines. This fact is illustrated in the following figure showing a wire with the length and direction $\vec{l}$ inside a magnetic field $\vec{B}$ under an angle $\alpha$ with respect to the field lines. We now want to derive the force that acts on a single charge $q$, an electron for instance. Since the current $I$ is created by the electrons moving inside the wire, the length $\vec{l}$ can be replaced with $\vec{l} = \vec{v}t$ and the current with $I=q/t$. Inserting these two equations leads to the very important and well-known Lorentz force: $$\boxed{\vec{F}_\mathrm{L} = q\vec{v}\times\vec{B}}$$ If there is only a single electron moving inside a magnetic field with the speed $v$ perpendicular to the field lines, the formula simplifies to $$F_\mathrm{L} = evB$$ Due to the fact, that the force acts perpendicular to the velocity vector, it can be treated as a centripetal force. The electron trajectory will therefore be bent to a circle. In order to calculate the radius $R$ of the circle, it is possible to equal the formulas for the centripetal force and Lorentz force: $$evB = \frac{mv^2}{R}$$ Solving this equation to $R$ leads to $$\boxed{R = \frac{mv}{eB}}$$ By replacing $mv$ with the momentum $p$, the resulting formula is even valid for relativistic particles: $$R = \frac{p}{qB}$$ It is therefore used for determining the momenta of particles with the charge $q$ created in particle collisions in the field of high energy physics.