Wheatstone Bridge

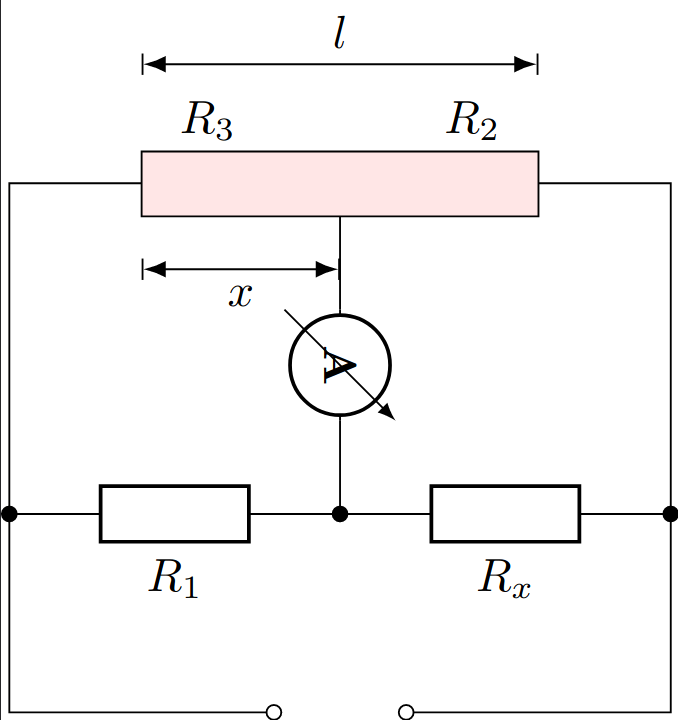
In addition to measuring currents and voltages, it often happens that resistance values ​​have to be measured. The so-called Wheatstone bridge circuit provides a precise procedure. A sliding wire potentiometer is usually used for this purpose, which represents a variable voltage divider whose resistance value can be continuously adjusted via a sliding contact, since the resistance increases in proportion to the length of the wire. The circuit then contains a fixed resistor $R_1$ (comparison resistor), a potentiometer with the values ​​$R_2$ and $R_3$, and the unknown resistor $R_x$. For the voltage dropping across resistor $R_1$, $U_1$ results $$U_1 = U_0\frac{R_x}{R_1 + R_2}$$ and analogously for $U_2$ $$U_2 = U_0\frac{R_2}{R_1 + R_2}$$ The current through the ammeter vanishes exactly when these two voltages are identical. Equating and transforming thus provides the following condition: $$R_x = \frac{R_1R_2}{R_3}$$ The ratio of the two resistors $R_2$ and $R_3$ can be set using the slide wire bridge with the length $l$ and the position of the slide wire $x$: $$\frac{R_2}{R_3} = \frac{l-x}{x}$$ This results in the calculation of the unknown resistance: $$\boxed{R_x = R_1\frac{l-x}{x}}$$ If the total length $l$ is known, only the partial distance $x$ needs to be measured once the potentiometer is adjusted so that the ammeter no longer reads current.