Angular Momentum
Definition of Angular Momentum
In this section, we want to transfer Newton's second law
$$\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}$$
to rotations and start with the definition of the
angular momentum.
Angular Momentum
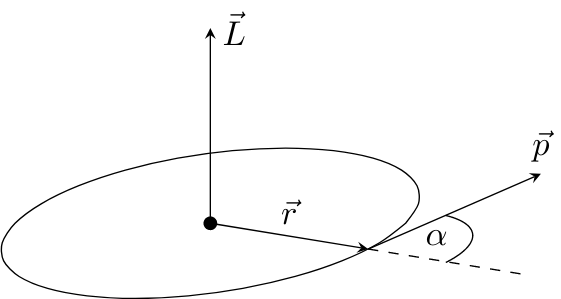
The angular momentum is defined as the cross-product of the distance vector $\vec{r}$ and the momentum $\vec{p}$:
$$\vec{L} = \vec{r}\times \vec{p}$$
This definition is similar to the previously described torque that was given as $\vec{M} = \vec{r}\times\vec{F}$.
Relationship with Torque
If we calculate the derivative of $\vec{L}$ with respect to the time, it follows
$$\frac{\mathrm{d}\vec{L}}{\mathrm{d}t} = \frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\times \vec{p} +\vec{r} \times \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}$$
Because $\mathrm{d}\vec{r}/\mathrm{d}t = \vec{v}$ points into the same direction as $\vec{p}$, the first part of the sum vanishes. Together with $\mathrm{d}\vec{p}/\mathrm{d}t = \vec{F}$ it follows
$$\frac{\mathrm{d}\vec{L}}{\mathrm{d}t} = \vec{r}\times \vec{F}$$
which is exactly matching with the definition of the torque. Hence, we can formulate the following statement:
Torque & Angular Momentum
An applied torque $\vec{M}$ can be expressed as the derivative of the angular momentum $\vec{L}$ with respect to the time $t$:
$$\vec{M} = \frac{\mathrm{d}\vec{L}}{\mathrm{d}t}$$
This equation also says that torque has to be applied to change the angular momentum of an object. Or in other words, if there is no torque acting on a rotating system, the angular momentum is conserved, similar to the momentum for translations:
Conservation of Angular Momentum
In a closed system without applying any torque, the angular momentum is conserved:
$$\vec{L} = \mathrm{const}$$
This conservation of the angular momentum is the reason, why the rotation frequency of our earth does not slow down or the moon continuously orbits around our planet.
Discussing Examples
We will discuss this phenomenon with the help of a simple example. Imagine an object circulating with a radius $r$ around a fixed point. The angular moment of this object can be calculated directly with its definition $\vec{L} = \vec{r}\times\vec{p}$ by replacing $\vec{p}$ with the product $m\vec{v}$. For a circular motion, the vectors $\vec{r}$ and $\vec{v}$ are perpendicular to each other. We can therefore write the absolute value of the angular momentum as
$$L = rmv$$
Now we can replace the speed $v$ with the product of the angular speed $\omega$ and the absolute value of the radius $r$ which leads to
$$L = m\omega r^2$$
This equation shows that the angular momentum of this object depends only on the angular speed and the radius. If the radius of the circular track decreases, e.g. by pulling the object towards the center, the conservation of the angular momentum leads to an increase in the angular speed. This effect is commonly used by ice skaters when they perform
pirouettes. Initially, both their arms are widely spread. After reaching the final angular speed, they draw the arms back towards their bodies and the angular speed increases drastically. The same effect can be reproduced at home with the help of a revolving office chair and heavy objects, such as books or barbells.
This page contains 689 words and 4081 characters.
Last modified: 2022-10-01 17:09:33 by mustafa