Buoyancy

• The buoyancy $F_B$ of an object in a fluid is equal to the weight $F_G$ of the displaced fluid: $$F_B = F_G$$
• If $\varrho_o$ is the density of the object and $\varrho_l$ the density of the liquid/gas, then the object sinks for $\varrho_o > \varrho_l$, floats for $\varrho_o = \varrho_l$, and moves upwards under the condition $\varrho_o < \varrho_l$

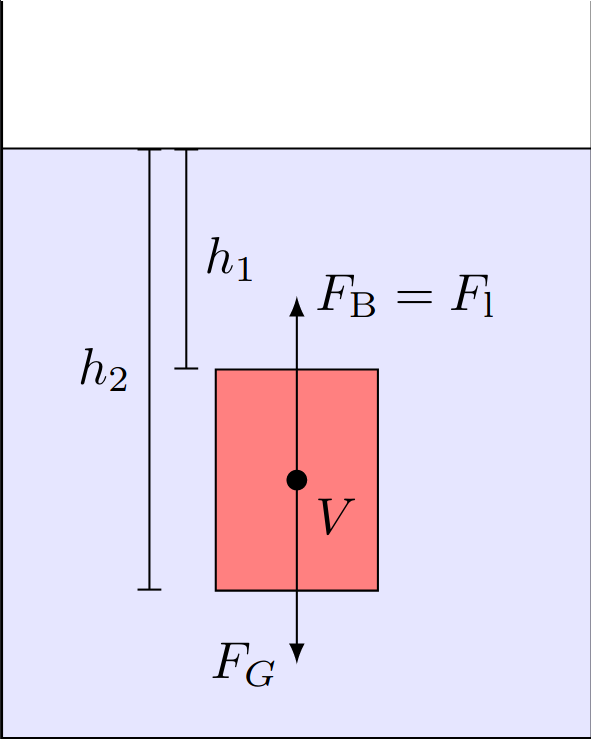
If the volume of a cuboid is placed in a fluid, a hydrostatical pressure acts on all its sides. While all forces compensate each other on the front and back as well as on the left and right side, the pressure on the top side with a distance of $h_1$ to the water surface can be calculated according to $$p_1 = \varrho g h_1$$ For the bottom side with the distance $h_2$ it can be calculated in an analog way: $$p_2 = \varrho g h_2$$ The difference between both pressures is then given as $$\Delta p = p_2 - p_1 = \varrho g \Delta h$$ with $\Delta h = h_2 - h_1$. Multiplying this with the area $A$ of the top and bottom surface, it follows for the force difference: $$F = \Delta p A = \varrho g V$$ The product of $V$ and $\varrho$ is equal to the mass of the displaced fluid. Hence, the buoyancy is given as the weight of the displaced liquid/gas. This is called Archimedes' principle and can be written as $$\boxed{F_B = F_G}$$ One can mathematically show that although this formula was derived for cuboids, it can be applied to all forms of objects. Archimedes' principle is therefore a universal law for calculating the buoyancy of any given object. However, it has to be taken into account that we assumed our fluid to be incompressible which is true for most liquids, although their compressibility is usually by a factor of 10 larger than solids. The compressibility of gases can be 10,000 times greater than liquids. In these cases, the derived formula can only be treated as an approximation. If a body is placed into a liquid, two forces are acting on it: the gravitational force $F_G$ dragging it downwards, and the buoyancy $F_B$ pulling the object in the exact opposite direction. Due to this reason, we can ignore the vector properties of both quantities and simply note down the total force $F_\mathrm{res}$ as the difference between both absolute values: $$F_\mathrm{res} = F_G - F_B$$ If $F_G$ is greater than $F_B$, the resulting force is positive, i.e. the body sinks. If, on the other hand, $F_B > F_G$, then the resulting force is negative and the object is pushed upwards. The interesting case is where $F_B$ and $F_G$ are equal: $$F_G = F_A$$ In this case, the resulting force $F_\mathrm{res}$ is 0, and the body floats in the liquid. Hence, it does not change its position unless it is pushed or pulled by external forces. We want to replace both forces by using the formula $F=mg$. The mass $m$ can be expressed as the product of the density $\varrho$ and the volume $V$. If we assign the index $o$ to the object and $l$ to the liquid, then we get $$\varrho_oV_og = \varrho_lV_lg$$ Of course, both volumes $V_0$ and $V_l$ must be equal. We can then cancel out $g$ and $V$ which leads to the following important statement: $$\boxed{\varrho_o = \varrho_l}$$ This equation says that an object floats in a liquid if its density equals the one of the liquid. As an example, we can take a look at a plastic cube with a density slightly larger than the one of water. Polystyrene in its solid form for instance can have a density up to $1050\,\mathrm{kg}/\mathrm{m}^3$, whereas water has a density of around $997\,\mathrm{kg}/\mathrm{m}^3$. After placing the cube in the water, it immediately sinks down. Now we insert salt into the water and as soon as the density of the liquid equals the one of the cube, it starts to float. If we increase the density even further, the plastic cube will be pushed upwards, until some parts are shown above the water surface.