Centripetal Force

If you bind a rope around an object (e.g. a stone) and you start to rotate it, you find out that it will move in a circular shape around your hand. If the object was not connected to the wire, it would move on a linear trajectory due to its inertia according to Newton's second law. Hence, in order to keep it on this circular track, your hand must provide a force which is called centripetal force. A formula to calculate this force quantitatively can be derived in several ways. In many textbooks, you will find a geometrical or mathematical approach. We will focus now on the latter one and describe the motion of the object in a two-dimensional cartesian coordinate system. 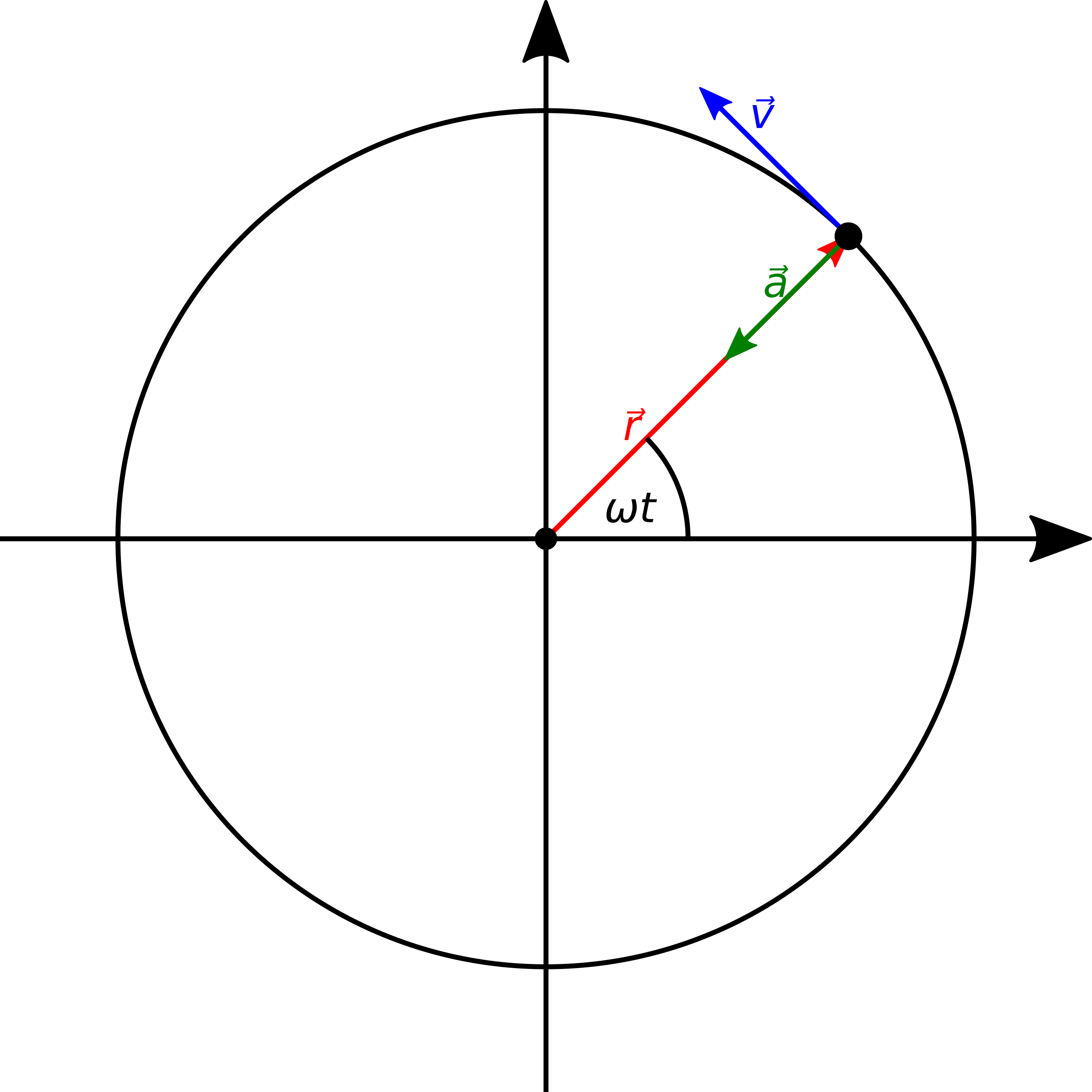First, we will write the vector $r$ by transforming the polar coordinates $r$ and $\alpha$ into cartesian coordinates: $$\vec{r} = r\begin{pmatrix}\cos\alpha\\ \sin\alpha\end{pmatrix} = r\begin{pmatrix}\cos\omega t\\ \sin\omega t\end{pmatrix}$$ Here, the angle $\alpha$ has been substituted by the product of the angular velocity $\omega$ and the time $t$. For obtaining the momentary velocity of the object, the derivation with respect to the time has to be calculated: $$\vec{v} = \omega r \begin{pmatrix}-\sin\omega t\\ \cos\omega t\end{pmatrix}$$ The product $\omega r$ is equal to the absolute value $v$ of the velocity. Since the dot-product of $\vec{v}$ and $\vec{r}$ is 0, the velocity vector is oriented perpendicular to the position vector for a circular movement. The second derivative leads then to the accelaration of the object: $$\vec{a} = -\omega^2 r \begin{pmatrix}\cos\omega t\\ \sin\omega t\end{pmatrix}$$ The minus sign from the derivative of the trigonometric functions has been shifted to the front of the right side of the equation. As one can see immediately, both vector components of $\vec{a}$ and $\vec{r}$ are equal except for a factor, and the acceleration vector is anti-parallel to the position vector. Taking only the absolute values into account, this can be written as $$\boxed{a_\mathrm{C} = \omega^2 r}$$ This acceleration is therefore called radial acceleration. Multiplying this equaiton with the mass $m$ is used to obtain the so-called centripetal force: $$\vec{F}_\mathrm{C} = -m\omega^2 \vec{r}$$ Because this vector is always pointing to the center of the circle, usually only the absolute value of $F_\mathrm{C}$ is used: $$\boxed{F_\mathrm{C} = m\omega^2 r}$$ Another possibility to write this equation is to convert the angular speed $\omega$ into the tangential speed $v$ by multiplying $\omega$ with $r$. This leads then to $$\boxed{F_\mathrm{C} = m\frac{v^2}{r}}$$ It depends on the situation which equation has to be used. Therefore, it is very useful to memorize both of them. In our common language, the term centripetal force is used less often compared to centrifugal force which we will study now a bit deeper. If a driver wants to move with his car around a corner, the existence of a centripetal force is required to keep the car on its track. This centripetal force is created by the grip between the tires and the asphalt. The driver himself, who is sitting in the rotating system, feels a force pushing him outwards into the opposite direction of the centripetal force. Because it is a result of the inertia of the driver, it is therefore also called inertia force. However, one has to keep in mind that it is not a real force, but a so-called pseudo force because it is not observable in the non-accelerated system. There are many possibilities in daily life to experience the centripetal force. In addition to a car moving around a corner, many people experience the centrifugal force when sitting in a roundabout that rotates around its central axis and therefore pushes the people towards the outer rim.