Galilei Transformation

• The Galilei transformation is used to transform coordinates from one inertial system to another one.
• The transformation from S' to S is given as $$x = x' + vt\qquad t = t'$$
• The resulting equations do not preserve the speed of light.

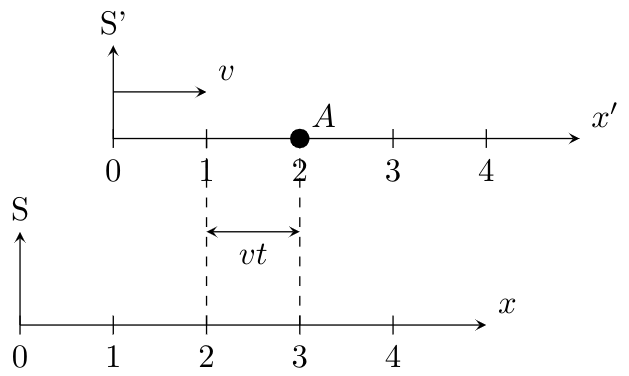
Let us take a look at two inertial systems S and S'. The system S is considered to be in rest, whereas S' moves with the speed $v$ relative to S. An object A may be fixed to the system S' at a position $x'$. In order to find the position in the system S, the following equation has to be used: $$\boxed{x = x' + vt}$$ If the system moves with a constant speed relative to another one, it can always be rotated in a way that it travels along the $x$-axis. It is therefore sufficient to concentrate only on one coordinate for the time being. If another B is fixed in S at a position $x$, then the transformation into the system $S'$ has to be done in the following way: $$\boxed{x' = x - vt}$$ However, these transformations can only be applied if the clocks in both systems to measure the time were synchronized before which means there is no time offset and for all positions, it can be written: $$\boxed{t = t'}$$ These three equations are usually called Galilei transformation, although they have been formulated by Isaac Newton at a later stage. The system S' can be for instance a train. If a person switches on a flashlight somewhere in the train and points into the direction of motion, then he will calculate the speed of light according to $$\frac{\Delta x'}{\Delta t} = c$$ which is of course equal to the well-known value $3\cdot 10^8\,\mathrm{m/s}$. An observer in the system S would then transform the coordinates of the light beam into his own system by using the Galilei transformation: $$\frac{\Delta x}{\Delta t} = \frac{\Delta x' + v\Delta t}{\Delta t} = \frac{\Delta x'}{\Delta t} + v$$ Taking the previous equation into account, this leads to $$\frac{\Delta x}{\Delta t} = c + v$$ This shows that the speed of light is not constant but dependent on the inertial system. This is, however, a contradiction to the observation made by Michelson and Morley. The Galileo transformation can therefore only be correct for small velocities $v \ll c$ and have to be replaced for larger speeds with a more general approach as it will be shown in the next section.