Golden Rule

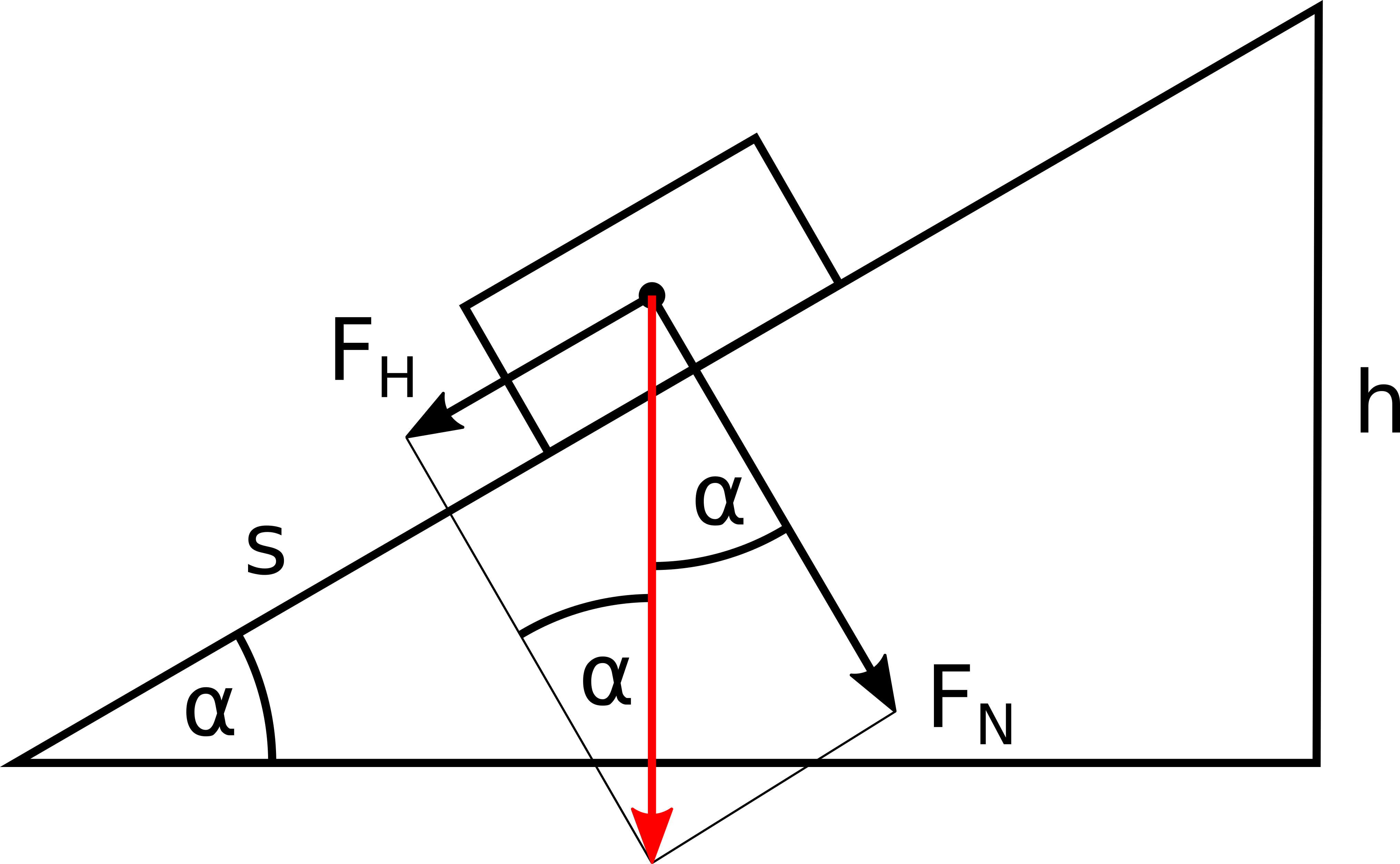
The energy of a system is defined as its ability to do work. It can exist in several forms, such as potential, kinetic, or thermal energy. In the following part, the term work will be defined. If a person wants to lift an object from the ground to the height $h$, the shortest distance is a vertical line. In this case, the uplifting force has to compensate for the full gravitation force $F_G$ acting on that object. To reduce the weight, the same object can also be transported via an inclined plane. Now only the downhill force $F_H$ has to be compensated which is by a factor of $\sin\alpha$ smaller than the gravitation force. However, the transportation path also increases from $h$ to $s$ which is by a factor of $\sin\alpha$ larger. This simple example shows that the product of $F$ and $s$ can be taken as a constant which has already been found by Galileo Galilei who formulated the "golden rule" of mechanics similar to the following statement: If you want to save force, you have to invest in the distance. After many disputes during centuries about the nature of this product, it was finally defined as a term called Work which is represented by the symbol W in formulas: $$W = F s$$ However, another result from that example is the fact that only the projection of the force into the direction of motion has to be taken into account. Mathematically, this is equal to the dot-product between the force vector and the position vector: $$W = \vec{F}\cdot\vec{r}$$ In a more general case, the force does not need to be constant over the full distance. In this case, it becomes a function of the position itself, leading to the following very important mathematical definition of the work: $$\boxed{W = \int \vec{F}(\vec{r})\cdot\mathrm{d}\vec{r}}$$ The unit of the work is $\mathrm{N\,m}$ according to its definition. However, this unit is usually replaced by Joule $\mathrm{J}$ to emphasize the fact that it is related to work. After carrying out this work, the object gains the same amount of energy. Therefore, work and energy are quantitatively equal and share the same unit.\par