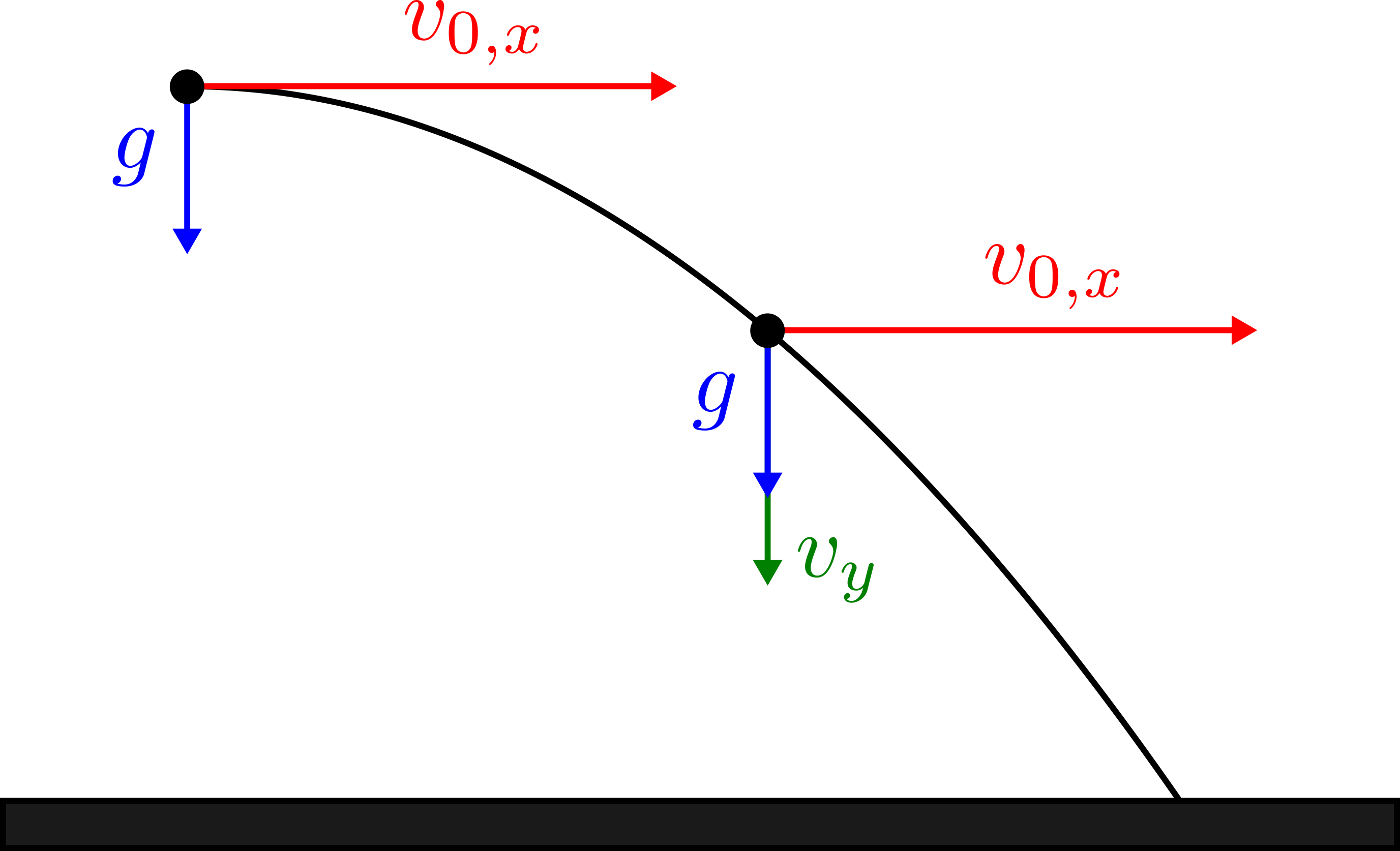
Horizontal Shot

The following sketch shows the trajectory of an object moving in the gravitational field of the earth after being shot in the horizontal direction: A horizontal shot takes place if the initial speed $v_{0,x}$ does not point into the $y$-direction but along the $x$-axis. Both directions can be treated completely independently because the movement in the $x$-direction does not affect the movement in the $y$-direction or vice versa. In this case, two equations of motions for both directions have to be solved simultaneously: $$x(t) = v_{0,x} t$$ $$y(t) = -\frac{1}{2}gt^2 + h$$ The easiest way to solve this equation system is to solve the upper equation for $t$ and insert it into the lower one which eliminates the time and results in a function of $x$: $$\boxed{y(x) = -\frac{1}{2}g\frac{x^2}{v_{0,x}^2} + h}$$