Hydrostatic Pressure

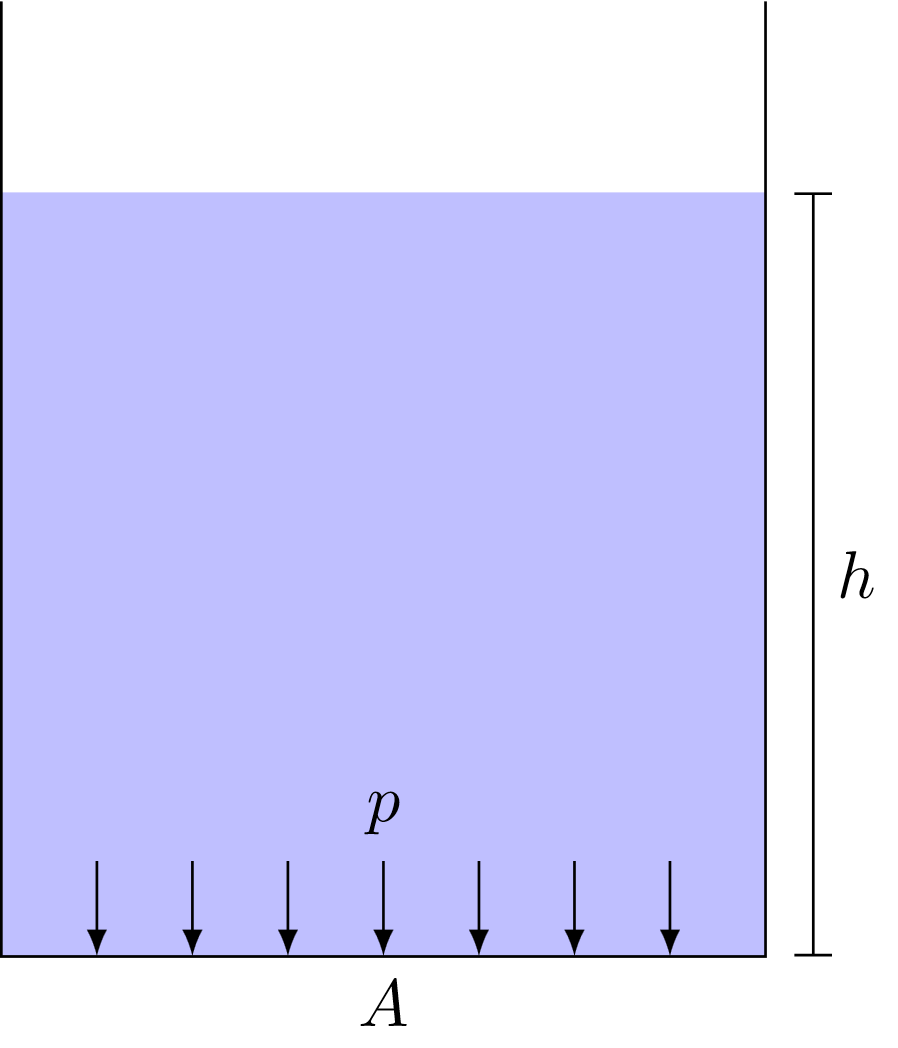
We want to calculate now the pressure of an incompressible liquid at a given depth below its surface. For this purpose we assume a volume to be filled with that liquid up to a height $h$ as illustrated in the figure below. The area of the volume is here denoted with $A$. If a volume is filled with water, then the weight on the bottom of this volume is given as $$F_G = mg$$ where $m$ is the mass of the water which can be replaced with the product of its density $\varrho$ and the volume $V$: $$F_G = \varrho V g$$ The volume, however, is equal to the product of the area $A$ and the height of the water level: $$F_G = \varrho A h g$$ Dividing both sides of the equation by $A$ leads to the pressure $p=F/A$ that acts at the bottom of the water volume due to the gravitational force: $$\boxed{p = \varrho g h}$$ Therefore, the pressure only depends on the height and not on the shape of the water volume. This behavior is called the hydrostatical paradox.