Potential Energy

• An object lifted upwards in the gravitational field of the earth gains potential energy.
• The potential energy is independent of the path and simply given as the product of the weight and height: $$E_\mathrm{pot} = mgh$$

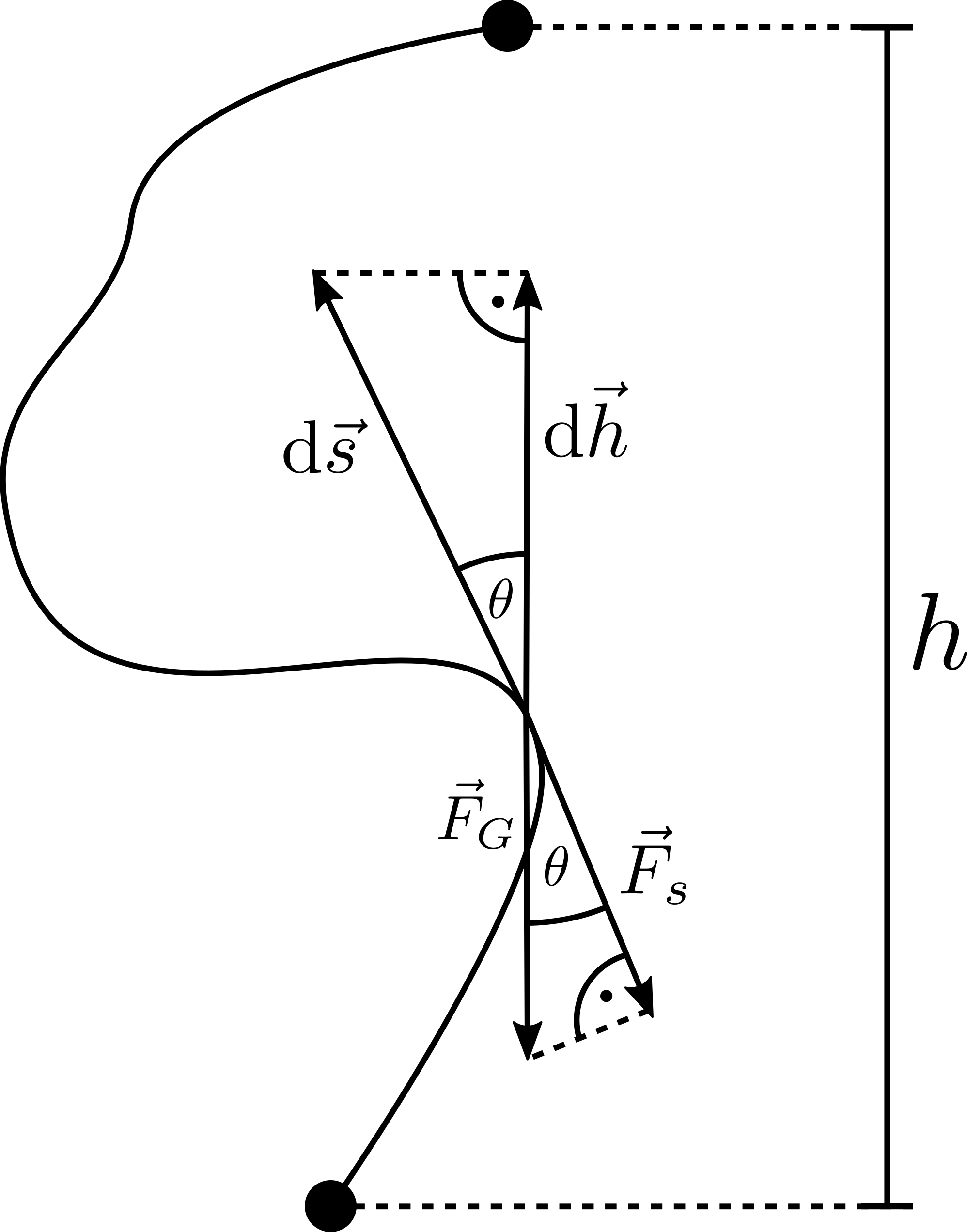
We have already seen in the example of the inclined plane that the work is independent of the path and only depends on the height. This fact will now be proven for arbitrary curves in the gravitational field of the earth near its surface. According to the definition of the work, the dot-product can then be written as follows: $$W = \int_{s_1}^{s_2} \vec{F}\cdot\mathrm{d}\vec{s} = \int_{s_1}^{s_2} F\cos\theta\,\mathrm{d}s$$ The correlation between the infinitesimal height $\mathrm{d}h$ and the infinitesimal path $\mathrm{d}s$ is given as: $$\mathrm{d}s = \frac{\mathrm{d}h}{\cos\theta}$$ Inserting this equation and integrating it over the full height leads to $$W = mgh$$ For the potential energy it follows then automatically: $$\boxed{E_\mathrm{pot} = mgh}$$ The important fact is that the amount of energy is independent of the actual path on which the object is lifted. It only depends on the height difference.