Projectile Motion

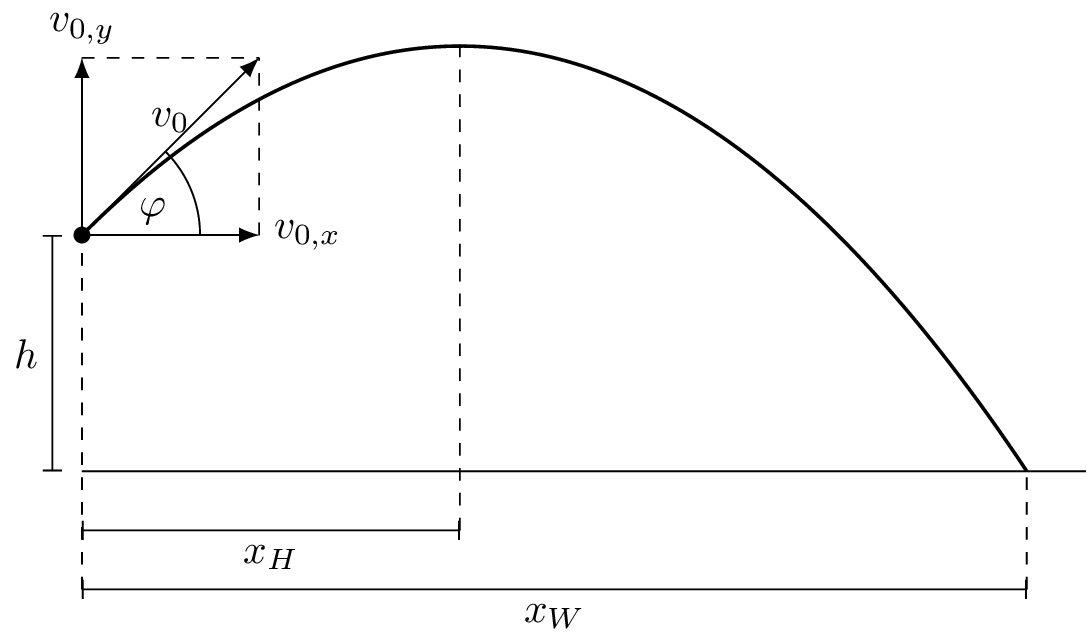
The following figure shows the important quantities that are used to describe the motion of the projectile. Let us assume a person throwing a stone from the height $h$ under the angle of $\varphi$ relative to the surface of the earth. The initial speed after the acceleration of the stone is given as $\vec{v}_0$. In the first step, we can decompose the velocity into the following two components: $$v_{0,x} = v_0\cos\varphi$$ $$v_{0,y} = v_0\sin\varphi$$ The resulting equations of motions are then given as $$x(t) = v_0\cos\varphi\,t$$ $$y(t) = -\frac{1}{2}gt^2 + v_0\sin\varphi\,t + h$$ Solving the first equation for $t$ and inserting it into the second one leads to the following quadratic correlation between the motion alone the $y$-axis and in $x$-direction: $$\boxed{y(x) = -\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\varphi} + x\tan\varphi +h}$$ The maximum distance can be obtained by equating this function with 0: $$y(t) = 0 \Leftrightarrow -\frac{1}{2}gt^2 + v_0\sin\varphi\,t + h = 0$$ The solution of this quadratic equation is given as: $$\boxed{t_\mathrm{W} = \frac{\sqrt{\sin^2\varphi\,v_0^2 + 2h}+v_0\sin\varphi}{g}}$$ Again, only positive values of $t$ are considered. Inserting this equation back into the formula for $x(t)$ leads to the distance at which the stone hits the ground: $$\boxed{x_W = v_0\cos\varphi \frac{\sqrt{\sin^2\varphi\,v_0^2 + 2h}+v_0\sin\varphi}{g}}$$