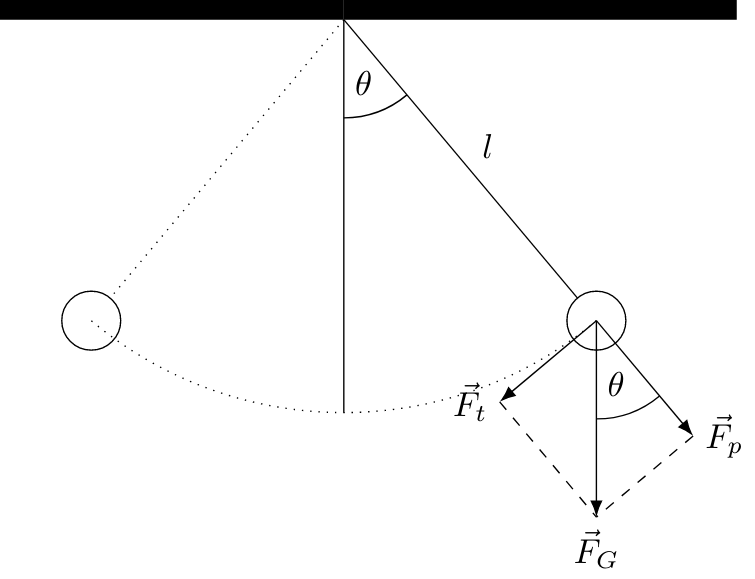
Simple Pendulum

The gravitational force can be decomposed into two components: one force $\vec{F}_t$ tangential to the motion and one force $\vec{F}_p$ perpendicular to it. The force, that causes the pendulum to oscillate, is, therefore, equal to $\vec{F}_t$ which is connected with the $\vec{F}_G$ via $$F_t = F_G\sin\theta$$ The equation of motion is similar to the spring pendulum given as $$m\ddot{x} = F_G\sin\theta$$ Because the pendulum can only move on a circular track, polar coordinates can be used which leads to the replacement $$\ddot{x} = l\ddot{\theta}$$ Together with the $F_G = mg$, it follows for the equation of motion $$\ddot{\theta} = \frac{g}{l}\sin\theta$$ At the moment we concentrate only on small amplitudes for which $\sin\theta$ can be approximated with $\theta$ which leads to $$\ddot{\theta} = \frac{g}{l}\theta$$ The same ansatz $$\theta(t) = A\sin\omega t$$ can be made, where $\omega$ is now given as the fraction $g$ over $l$. The period of a simple pendulum can then be calculated according to $$T = 2\pi\sqrt{\frac{l}{g}}$$ In this equation, $l$ represents the length of the pendulum and $g$ the gravitational acceleration. The important and maybe not obvious result is that the period of time is independent of the amplitude and the mass that has been attached to the thread.