Speed & Velocity

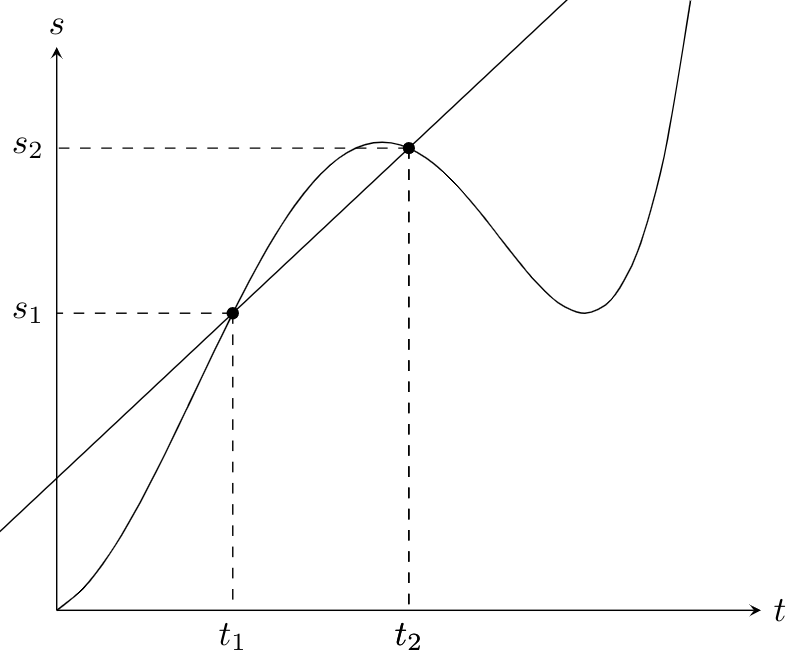
The speed of an object is defined as the changing of its position with respect to the time interval. If an object is at a position $s_1$ at a time $t_1$ and later at another position $s_2$ at the time $t_2$, then the speed is calculated according to: $$v = \frac{s_2 - s_1}{t_2 - t_1}$$ Each minus sign can also be replaced with a $\Delta$ which results in $$\boxed{v = \frac{\Delta s}{\Delta t}}$$ However, one has to take into account that this formula does describe only the actual speed of an object if it travels at a constant speed. Otherwise, the resulting value is the average speed. This can be displayed with the help of a so-called space-time diagram or $s$-$t$-diagramm. 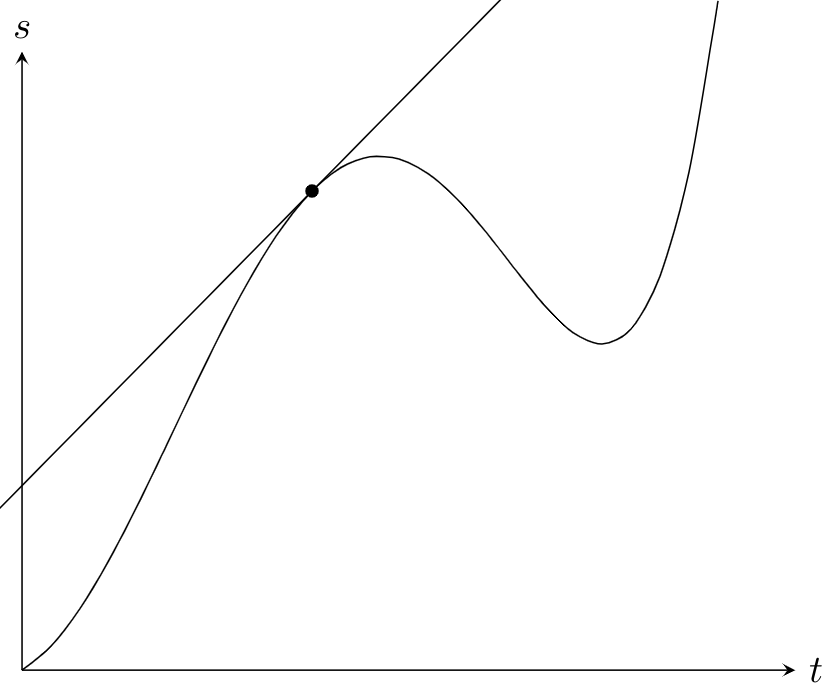In order to determine the momentary speed of an object, the limit of infinitesimally small time intervals $\Delta t\rightarrow 0$ has to be calculated: $$v= \lim_{\Delta t\rightarrow 0}\frac{\Delta s}{\Delta t}$$ This leads to the derivative of $s$ with respect to $t$: $$\boxed{v = \frac{\mathrm{d}s}{\mathrm{d}t}}$$ If you want to calculate the velocity of an object, you have to additionally take the direction of motion into account, because an object can also move in a two-dimensional or three-dimensional world. In this case, the position $s$ transforms into the position vector $\vec{r}$ which includes one entry for each coordinate: $$\vec{r} = \begin{pmatrix} x\\y\\z\end{pmatrix}$$ The average velocity $\vec{v}$ as being a vector quantity is then simply defined as the division of each component difference by the time interval. This can be written as follows: $$\vec{v} = \begin{pmatrix}\frac{\Delta x}{\Delta t}\\ \frac{\Delta y}{\Delta t}\\ \frac{\Delta z}{\Delta t} \end{pmatrix}= \frac{\Delta \vec{r}}{\Delta t}$$ If the object does not move with a constant speed, and we are interested in the momentary velocity, then the derivative of the position vector with respect to the time has to be calculated. This can be written in the following form: $$\boxed{\vec{v} = \frac{\mathrm{d}\vec{r}}{\mathrm{d}t}}$$ This equation states that the first derivative of every component of the position vector has to be calculated individually. In order to receive the speed $v$ of an object moving with the velocity $\vec{v}$, the absolute value has to be calculated which can be written as the square-sum of all three components: $$v = |\vec{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2}$$ In the next step, we also want to find a method to convert km/h into m/s. For that purpose, we can write $$1\frac{\mathrm{km}}{\mathrm{h}} = 1,000\,\frac{\mathrm{m}}{\mathrm{h}} = \frac{1,000}{3,600}\,\frac{\mathrm{m}}{\mathrm{s}} = \frac{1}{3.6}\,\frac{\mathrm{m}}{\mathrm{s}}$$ This equation shows that in order to obtain the speed of an object in km/h, the value in m/s has to be multiplied with 3.6: $$v\left[\frac{\mathrm{km}}{\mathrm{h}}\right] = 3.6\cdot v\left[\frac{\mathrm{m}}{\mathrm{s}}\right]$$ On the other hand, a given value in km/h has to be divided by 3.6 to receive the speed in m/s.