Standing Waves

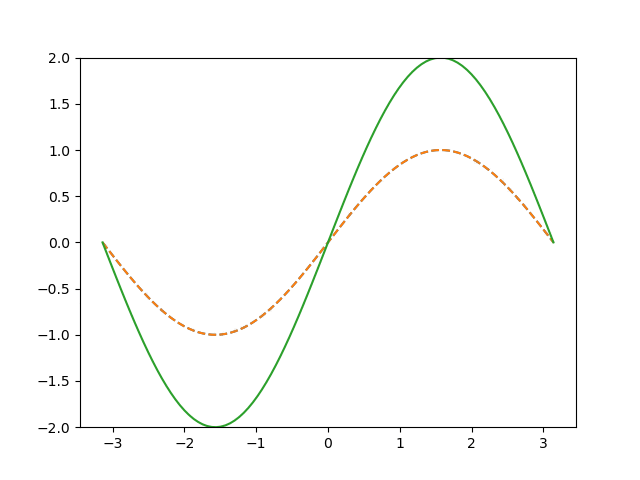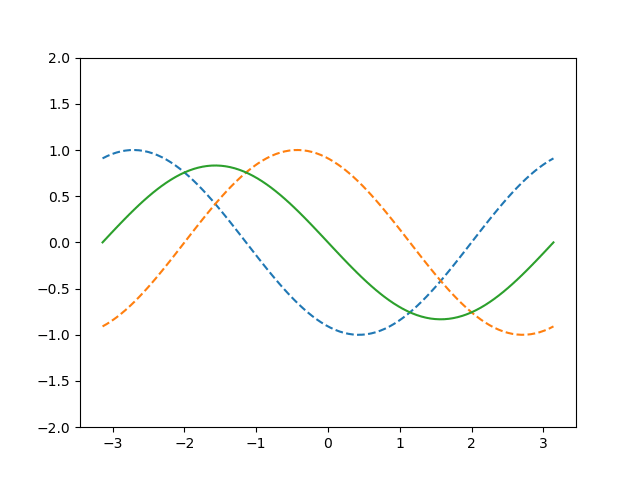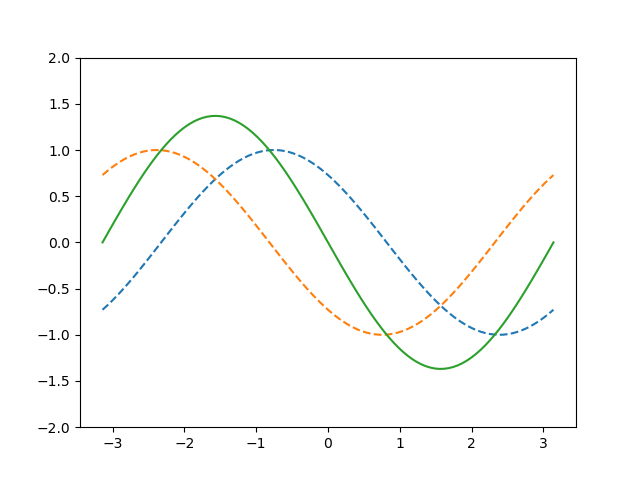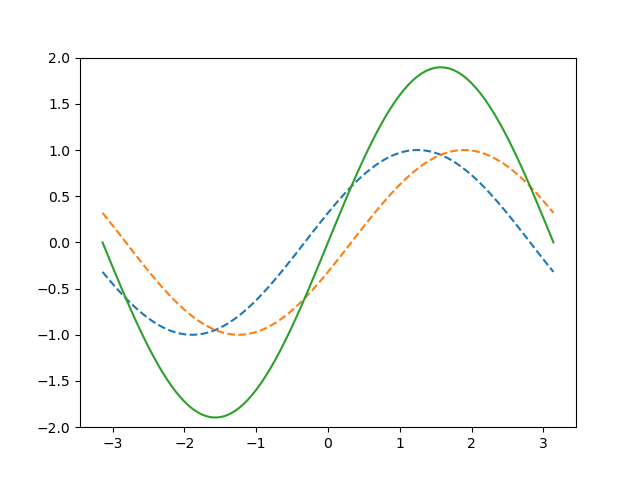
Standing waves are created when a wave coming from one side $$\psi_1(x,t) = A\sin(\omega t - kx)$$ interact with waves entering from the other side $$\psi_1(x,t) = A\sin(\omega t + kx)$$ The new resulting wave is the therefore the sum of both elongations $\psi_1$ and $\psi_2$ at each timestamp. The addition theorem for the sine then leads to $$\psi(x,t) = A\sin(\omega t) \cos(kx)−A\cos(\omega t) \sin(kx) +A\sin(\omega t) \cos(kx) +A\cos(\omega t) \sin(kx)$$ Some of these terms cancel out and only the follwing part remains: $$\boxed{\psi(x,t) = 2A\sin(\omega t)\cos(kx)}$$ This function describes an oscillator with a time-dependent elongation $2A\sin\omega t$ and an oscillation in space given by $\cos kx$. The amplitude of the standing wave is therefore two times larger than the ones of the original waves. This result can be interpreted as follows: A harmonic wave is entering from the left, while another one enters from the right. This could either be a second wave or a reflection of the first one. The sum of these elongation does not move in space anymore. Instead, it contains nodes, where no elongation takes place, and loops with maxima and minima. The animation of such a standing wave can be seen below: The two original waves are illustrated with dashed lines, whereas the solid one shows the superposition of both of them, resulting in a standing wave. Standing waves occur in many situations, e.g. with strings of musical instruments like guitars. When the string oscillates, the created wave is reflected on both sides and create a standing wave.