Time Dilation

• A clock moving relative to an observer at rest runs slower from the observer's point of view than a clock in the observer system.
• The relation between $\Delta t$ in the observer system and $\Delta t'$ in the moving system is given as $$\Delta t = \frac{\Delta t'}{\sqrt{1-\frac{v^2}{c^2}}}$$

We assume an observer to be at rest in the inertial system S. This observer can measure the time by looking at a clock that rests in his system. Now this observer sees the time shown by a clock in the system S' that moves with the speed $v$ relative to the observer system S. The observer finds out that the time in S' runs slower than in his own rest frame. This effect is called relativistic time dilation. There are actually two ways to derive a quantitative relation between the time $\Delta t$ in the observer system and $\Delta t'$ in the moving system: a geometrical approach including a thought experiment with light clocks and an algebraic one using the previously derived Lorentz transformation. We first want to start the latter one. The observer rests in S at the position $x_0$ and observers two light pulses emitted at the times $t_1$ and $t_2$. The measured time difference between these two pulses for the observer is therefore given as $$\Delta t = t_2 - t_1$$ However, an observer in the moving system S' measures the two timings $t_1'$ and $t_2'$ for receiving the light pulses. For the observer in S, these timings transform according to the Lorentz transformations of time: $$t_1 = \gamma\left(t_1' - \frac{vx_0'}{c^2}\right)$$ $$t_2 = \gamma\left(t_2' - \frac{vx_0'}{c^2}\right)$$ Therefore, it follows for the time difference $t_2 - t_1$ in the moving system S $$\Delta t = \gamma \Delta t'$$ Since the Lorentz factor is always larger than $1$, the measured time for an observer in S is always larger. This effect is called time dilation. It can be summarized with the sentence "Moving clocks tick slower". To understand this phenomenon a bit deeper we want to introduce a fictional light clock that does not exist in reality but is commonly used to derive and check certain results in special relativity. A light clock is therefore a thought experiment that consists of a box with mirrors on the top and bottom. Inside the box, a light pulse is continuously reflected between these two mirrors. Every time it hits the bottom mirror, a time signal is generated, and the accumulated time can be read from a display attached to the clock. 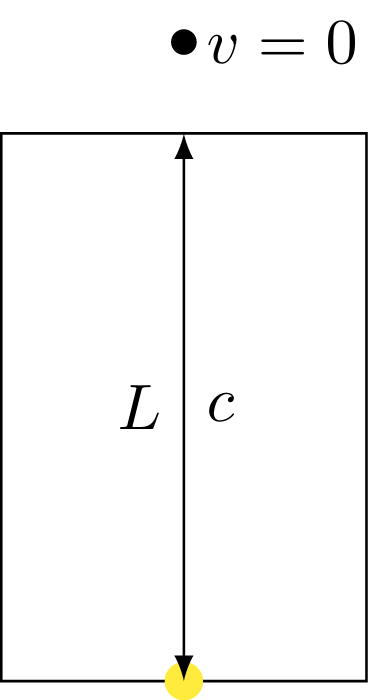Now we want to see what happens if the clock moves with the speed $v$ perpendicular to an observer that rests in a system S. 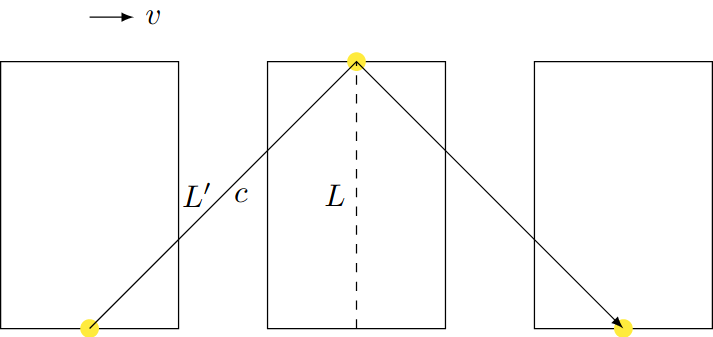If the height of the clock is given as $L$, then the time for half a time period for an observer in the reference frame S' of the clock is given as $$\Delta t' = \frac{L}{c}$$ For the observer in S, the pulse has to cover the longer path $L' = c^2\Delta t^2$. Since the total speed of light $c$ must be constant in any reference frame, we can immediately see that this must lead to a larger difference indicated by the clock. We can then use the Pythagorean theorem to write down the following relation for the half period: $$c^2\Delta t^2 = c^2\Delta t'^2 + v^2\Delta t^2$$ Now we bring all timings $\Delta t$ on one side: $$c^2\Delta t^2 - v^2\Delta t^2 = c^2\Delta t'^2$$ Dividing this equation by $c^2$ finally leads to $$\Delta t'^2 = \left(1-\frac{v^2}{c^2}\right)\Delta t^2$$ Now we can easily solve this equation for $\Delta t$ and receive the following important formula known as time dilation: $$\Delta t' = \frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}$$ We have already come across the inversed square root term and called it the Lorentz factor $\gamma$. The first experimental confirmation of this theoretical derivation was done by Joseph C. Haefele and Richard Keating in October 1971. Both US physicists synchronized some atomic clocks which already had a very high precision at that time. One group containing 4 atomic clocks was placed on the ground, whereas another group was placed in an airplane and traveled for 2 days around the equator in the eastern direction. A third group was placed in another airplane and traveled in the western direction. The main reason for using more than one clock in each system was the possibility to calculate average values. The equator and thus the clock placed on the ground moves at a speed of 1670 km/h. The airplane had a speed of around 800 km/h. The clocks in the airplane traveling in the eastern direction were therefore moving at a total speed of 1670 km/h + 800 km/h, whereas the one traveling in the western direction was moving at a speed of 1670 km/h - 800 km/h. Therefore, we expect a certain time difference as a result of the time dilation between both moving systems and the system attached to the earth. As a result of this experiment, the clock moving in the eastern direction showed a time difference of $$\Delta t_\mathrm{east} = (-255\pm 10)\,\mathrm{ns}$$, whereas the one moving in the western direction showed a difference of $$\Delta t_\mathrm{west} = (+77\pm 7)\,\mathrm{ns}$$ The measured time difference of a few nanoseconds was of course very small, but measurable with the equipment available at that time. If one uses only the derived formulas for the time dilation, it turns out that the measured time difference does not match exactly with the prediction. The reason can be found in the fact that according to the general theory of relativity gravitation has an additional influence on the measured time difference, and the clock in a system far away from the earth's surface would measure a time difference simply due to the absence of a gravitational field. And additionally, the rotating earth is not an inertial system. As a result, the predictions have to be tuned using more complex mathematical equations. Although there were doubts about the correctness of the experimental outcome at that time, this experiment can be seen as the first proof of time dilation in history.