Toricellis Law

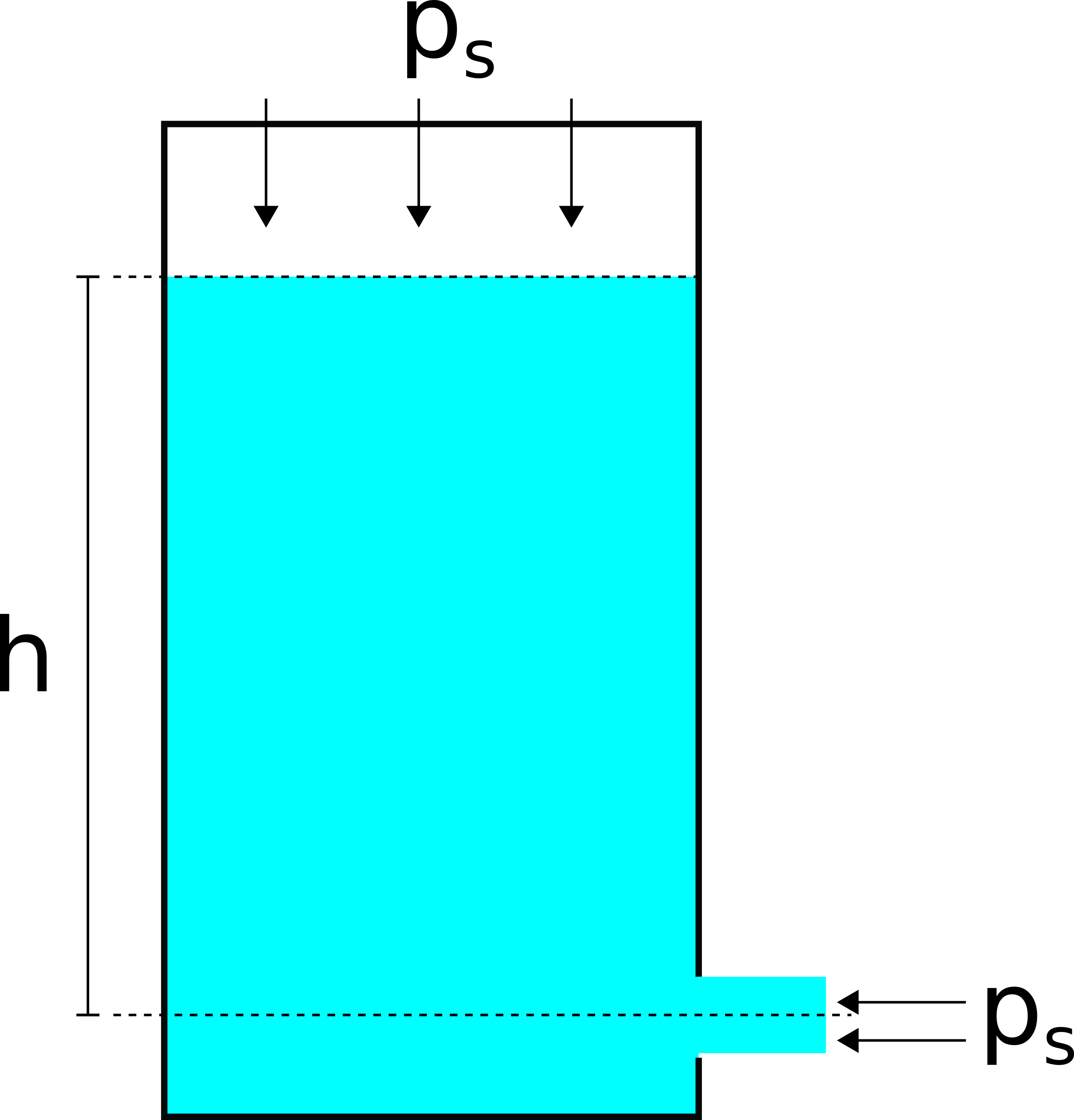
The working principle of Bernoulli's principle can be understood better in the following example: A bucket is filled with water and has a small hole above its ground as shown in the following figure: The pressure from the other molecules on top press the water through the hole. While the molecules inside the bucket can be assumed as being at rest, the molecules leaving the bucket through the hole have only kinetic energy. The static pressure $p_s$ due to the air pressure above the water surface is constant on both sides of the equation and therefore cancels out. This results in $$\frac{1}{2}\varrho v^2 = \varrho g h$$ Solving this equation for $v$ gives $$\boxed{v = \sqrt{2gh}}$$ which is equal to the previously derived speed of an object falling from the height $h$. This quantitative relation between the exhaust speed $v$ and the height $h$ is called Torricelli's law. However, it has to be taken into account that for the afore-mentioned derivation an infinitesimal small hole had been assumed. Now we take a look at a case, in which the diameter of the hole cannot be neglected anymore. If $A_1$ is the are the surface area of the bucket and $A_2$ the area of the hole, then the law of Venturi $$\frac{v_1}{v_2} = \frac{A_2}{A_1}$$ has to be applied which leads to $$v' = \frac{A_2}{A_1}\sqrt{2gh}$$ where $v'$ denotes the speed of the water surface in the bucket. Since this speed is equal to the derivative $\mathrm{d}h/\mathrm{d}t$ of the height, the following differential equation can be formulated: $$\frac{\mathrm{d}h}{\mathrm{d}t} = c\sqrt{h}$$ The constant values have been replaced with the constant $$c = -\frac{A_2}{A_1}\sqrt{2g}$$ This differential equation can be solved by separting the variables and integrating both sides: $$\int \frac{\mathrm{d}h}{\sqrt{h}} = c\int\mathrm{d}t + C$$ Calculating the integrals and solving the equation for $h(t)$ gives $$h(t) = \frac{1}{4}(ct + C)^2$$ The integration constant $C$ can be eliminated by inserting the boundary condition $h(0) = h_0$. Then the solution can be written as $$\boxed{h(t) = \frac{1}{2}\left(\frac{A_2}{A_1}gt^2\right) - \sqrt{2gh_0}\frac{A_2}{A_1}t + h_0}$$ Setting this function equal to $0$ and solving the resulting equation with second-degree order gives the time $$\boxed{T = \frac{A_1}{A_2}\sqrt{\frac{2h_0}{g}}}$$ for the bucket to be empty.