Torque

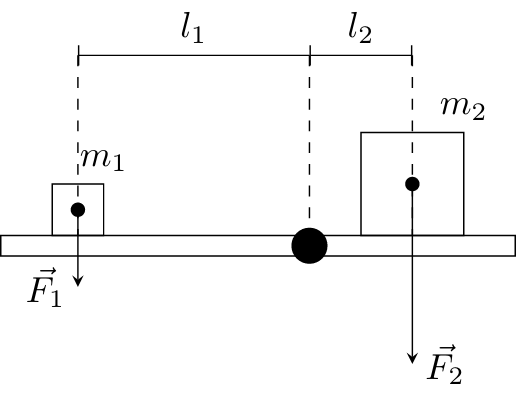
The laws, that we have derived for the translation of mass points shall now be transferred to rotations. We first take a look at a scale with a rod that is mounted in a way that it can be divided into two lever arms with the lengths $l_1$ and $l_2$. On side of the scale, a mass with the weight $F_1$ is placed in the distance $l_1$ to the mounting point. In order to balance the scale, a mass with the gravitational force $F_2$ has to act on the opposite lever arm with the length $l_2$. It turns out that the scale does not rotate if the product of $F_1$ and $l_1$ is equal to the one of $F_2$ and $l_2$. This is called the law of the lever. 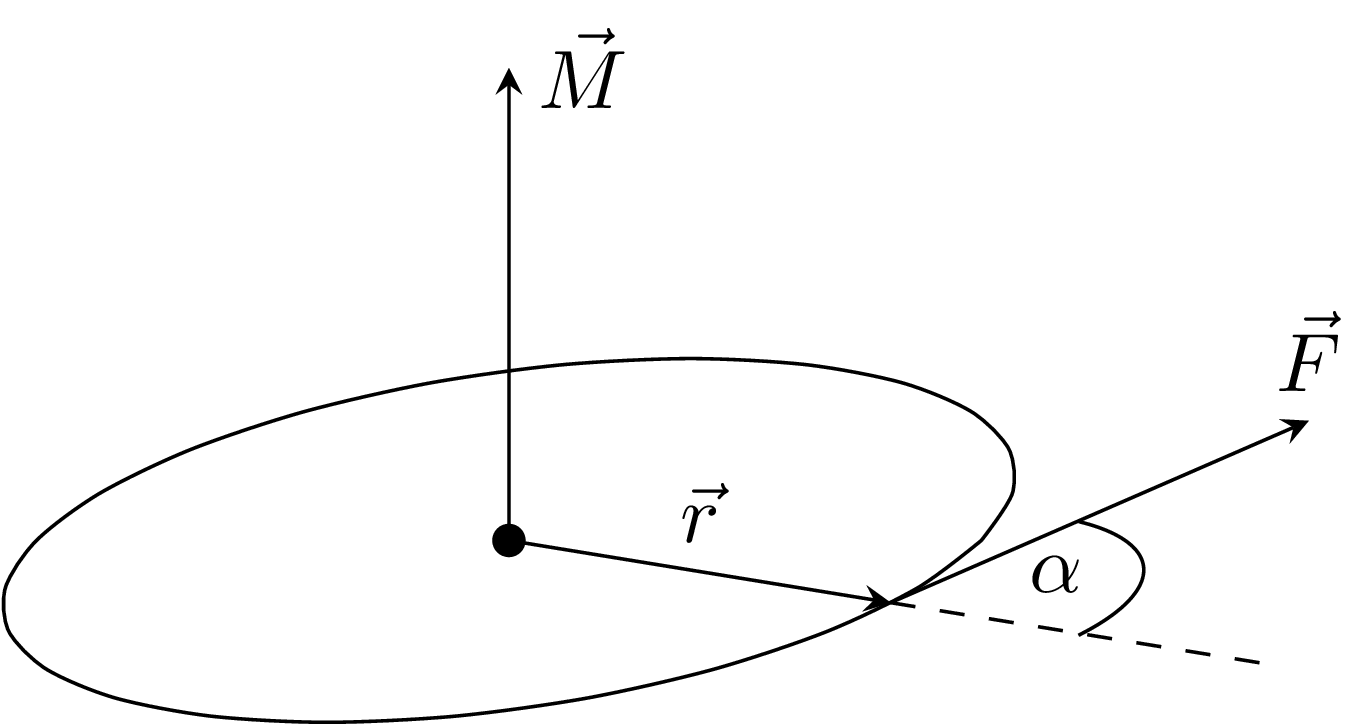If the forces act on the levers under certain angles $\alpha_1$ and $\alpha_2$, then only the components with a direction perpendicular to the lever arms have to be taken into account: $$F_\perp = F\sin\alpha$$ The other component is compensated by the lever itself. In three dimensions it is, therefore, useful to use the cross-product of the distance vector $\vec{r}$ and the force $\vec{F}$ and call that quantity torque. The quantity $\vec{M}$ is then called torque. Due to the cross-product, the direction of $\vec{M}$ is always perpendicular to the force vector $\vec{F}$ and the radius vector $\vec{r}$. The unit of the torque is $\mathrm{Nm}$, similar to the one of the energy.