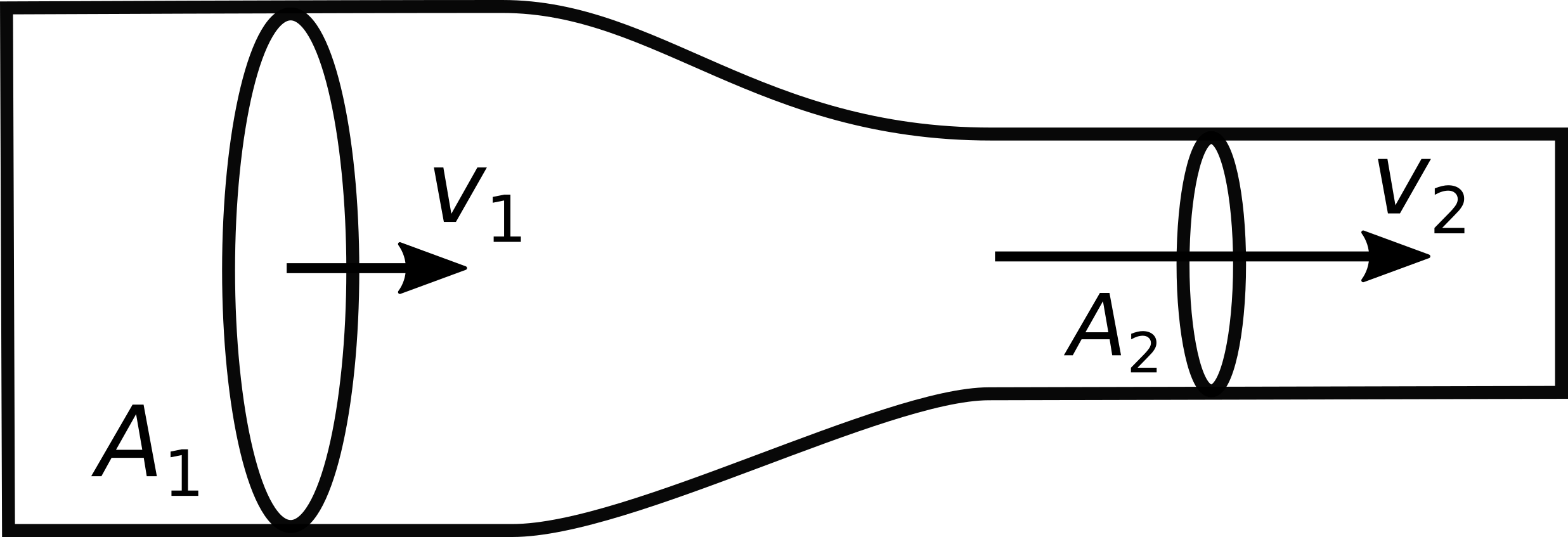
Volume Flow

The volume flow is defined as the derivative of the volume of a fluid with respect to time: $$\boxed{Q = \frac{\mathrm{d}V}{\mathrm{d}t}}$$ The volume can be substituted with $V = As$, where $A$ is the area of the pipe at a given position and $s$ the distance which the fluid travels within a certain time window. The derivation then leads to $$\boxed{Q = Av}$$ In a closed system, for instance, a pipe with different diameters, the volume flow has to be constant everywhere because if the fluid can be assumed to be incompressible: $$Q_1 = Q_2$$ This leads to the following equation: $$A_1v_1 = A_2v_2$$ or written in another way: $$\boxed{\frac{v_1}{v_2} = \frac{A_2}{A_1}}$$ This formula, which is sometimes called the Venturi effect, can be used to calculate the velocity of the fluid particles in different parts of the system. The following figure illustrates the behavior of incompressible fluids in a pipe with two different radii: In the second part of the pipe, the speed increases because the radius and therefore the area gets smaller.