Compton Effect

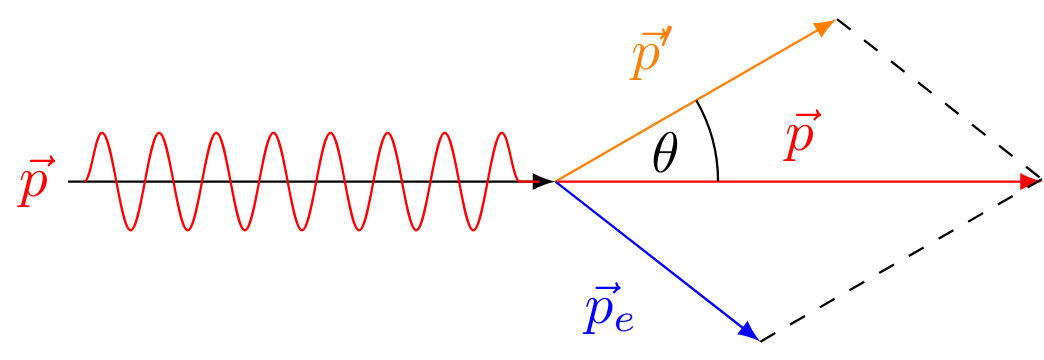
In the year 2022, A. H. Compton irradiated an object made of graphite with monochromatic X-rays. With the help of lead absorbers in the area, he was then able to measure only photons that were scattered under the angle $\theta$. The scattered photons then entered a crystal where they were undergoing Bragg diffraction. With this method, it was possible to determine the wavelength of the photons after the collision with the scattering object took place. Compton found that the wavelength of the scattered photons increased and therefore had smaller energy and momentum than the original ones. Compton interpreted this effect, which was later named after him, correctly as an elastic collision between the photon and the electron, similar to the collision of Billiard balls. The Compton effect can therefore be seen as the final proof that photons are quantum objects that carry energy and momentum. In order to derive a formula to calculate the wavelength change, we have to write down first a few equations. The first one is the energy conservation of the whole process, assuming the electron was at rest: $$E + E_0 = E' + E_e'$$ The quantities $E$ and $E_0$ denote the energies of the photon and electron before the collision took place. $E'$ and $E_e'$ represent then the energies of both particles after the collision. The momentum conservation can be written in vector form as $$\vec{p} = \vec{p'} + \vec{p}'_e$$ The momenta $p$ and $p'$ without an index stand for the momenta of the photon before and after the collision, whereas $\vec{p}'_e$ denotes the momentum of the electron after the collision. We can now calculate the absolute value of $\vec{p}'_e$ by using the dot product which then leads to the cosine law: $$p_e'^2 = p^2 + p'^2 - 2pp'\cos\theta$$ The relativistic energy-momentum relation can be written as $$E_e'^2 = E_0^2 + p_e'^2 c^2$$ In the next step, we have to rearrange the energy conservation according to $$E_e' = E+E_0-E'$$ and insert it into the energy-momentum relation: $$p_e' = \frac{E_e'^2 - E_0^2}{c^2} = \frac{(E+E_0-E')^2 - E_0^2}{c^2}$$ Together with $p$ and $p'$ we can insert it into the previously derived cosine law and get $$\frac{(E+E_0-E')^2 - E_0^2}{c^2} = \frac{E^2}{c^2} + \frac{E'^2}{c^2} - \frac{2EE'}{c^2}\cos\theta$$ Now we have to simplify the resulting equation a bit: $$E^2 + E_0^2 - E'^2 + 2EE_0 - 2EE' - 2E'E_0 - E_0^2 = E^2 + E'^2 - 2EE'\cos\theta$$ This then leads to $$2EE_0 - 2EE' - 2E'E_0 = -2EE'\cos\theta$$ and after a small rearrangement: $$\frac{1}{E'} - \frac{1}{E_0} - \frac{1}{E_0} = \frac{\cos\theta}{E_0}$$ Using the energy-momentum relation $E=pc$ for photons and the formula for the DeBroglie wavelength $p=h/\lambda$, we can now write: $$\frac{\lambda'}{hc} - \frac{\lambda}{hc} = \frac{1}{E_0}(1-\cos\theta)$$ or in a bit different way by multiplying both sides with $hc$: $$\lambda' - \lambda = \frac{h}{m_ec}(1-\cos\theta)$$ The difference between both wavelengths is usually denoted as $\Delta\lambda$. Additionally, the term $h/(m_ec)$ is usually called Compton wavelength $\lambda_C$. With these definitions, we can write down the following rule. The Compton wavelength has been defined for an electron, because of historical reasons. Of course, the Compton wavelength can also be calculated for any other particle, but in this case, the electron mass $m_e$ has to be replaced with the mass of the particle. Since the maximum scattering angle of the photon is $180^\circ$, the term $1-\cos\theta$ cannot exceed the factor 2, i.e. the maximum wavelength shift is twice the Compton wavelength of the electron. Starting from the previously derived formula for the wavelength shift, we want to calculate the energy loss of the scattered photon. For that purpose, we replace use again the relations $p=h/\lambda$ and $E=pc$ for photons. This leads to the following equation $$\frac{h}{E'}c - \frac{h}{E}c = \frac{h}{m_ec^2}(1-\cos\theta)$$ Now we can divide both sides by $h$ and $c$ and bring the term $1/E$ to the other side: $$\frac{1}{E'} = \frac{1}{m_ec^2}(1-cos\theta) + \frac{1}{E}$$ Then finally we only have to invert both sides leading to $$E' = \frac{1}{\frac{1}{m_ec^2}(1-\cos\theta)+\frac{1}{E}} = \frac{E}{1+\frac{E}{m_ec^2}(1-cos\theta)}$$ This formula is also called the Klein-Nishina formula. It provides a relation between the original photon energy and the energy after the collision with an electron took place. As one can see, the new energy does only depend on the original photon energy and the scattering angle. The energy of the electron is of course equal to the difference between the original photon energy and the energy after scattering: $$E_e' = E - E' = \left(1-\frac{1}{1+\frac{E}{m_ec^2}(1-cos\theta)}\right)$$ If someone wants to measure the energy of a photon in a detector, the energy transfer to an electron has to be determined. 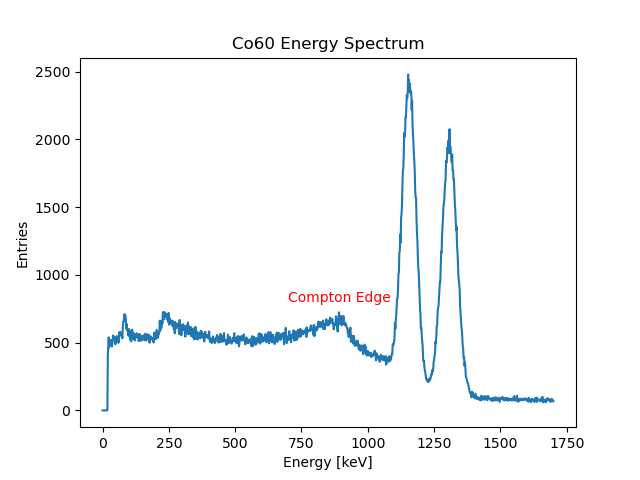The maximum scattering angle of $180^\circ$ for the photon refers to the maximum electron energy of $$E_e' = \frac{E}{1+\frac{2E}{m_ec^2}} = \frac{2E}{m_ec^2 + 2E} = \frac{E}{1+\frac{m_ec^2}{2E}}$$ The spectrum obtained from photons hitting a detector will therefore show a continuous, almost flat, distribution with a maximum transferable energy called Compton edge. In the case of a Co-60 source, the spectrum shows a Compton edge around 900 keV, a few hundred keV below the peak of the photo effects. Since it is very difficult to focus gamma rays using lenses, the Compton effect plays an important role in imaging using gamma-rays in the energy range from a few hundred keV to tens of MeV. In so-called Compton telescopes (also called Compton cameras), the energy and direction of the scattered photon as well as the energy and (sometimes) also the direction of the electron are measured. This leads to a determination of the energy, the direction of origin, and sometimes even the polarization of the incident photon. One of the best-known telescopes is COMPTEL, which was the first telescope to explore the starry sky in the energy range between 0.75 and 30 MeV on bord the CGRO satellite of NASA from 1991 to 2000. With this satellite, it was possible to create the first celestial maps in this energy range, research into nucleosynthesis, as well as advances in the study of pulsars, active galaxies (AGNs), etc. In the future, Compton cameras may provide a better spatial resolution in the field of medicine than the scintigraphy gamma cameras used today, i.e. localize tumors and metastases more precisely. In the future, Compton cameras could be used in nuclear technology such as nuclear plants to measure radioactive waste. For security checks at airports, scanner devices were developed which use Compton backscatter from X-rays on surfaces. These are currently being tested in the USA. The Compton effect can also be reversed, when an electron or any other charged particle collides with a photon and loses some of its energy by transferring it to the photon. This is called the inverse Compton effect which is used for instance to generate monochromatic, linearly polarized gamma rays by backscattering laser photons off high-energy electrons.

• Compton Wavelength of Proton (+)