Cavendish Experiment

Two masses $m_1$ and $m_2$ with a distance $r$ attract each other with a force $F_G$ due to gravitational interaction. The strength can be calculated with the help of Newton's gravitation law: $$\boxed{F_G = G\frac{m_{1}m_{2}}{r^{2}}}$$ The proportionality factor $G$ is called the gravitational constant. One can determine $G$ by measuring the values for $F_G$ for known masses $m_1$, $m_2$, and distances $r$ within a dedicated setup called the Cavendish experiment. 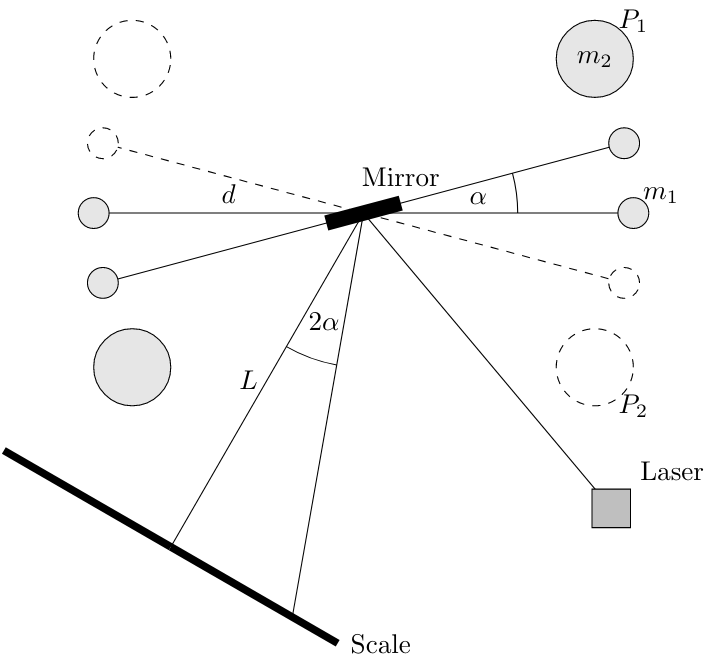Two small lead balls with the masses $m_1$ are attached to the ends of a thin rod. This rod is mounted horizontally to a thin vertical wire. In the absence of other masses, a certain resting position is occupied. If two large lead balls with the masses $m_2$ are brought close to these balls, then torques are generated by the gravitational forces acting on them. These lead to a twisting of the wire by an angle $\alpha_0$ which is going to be measured by a small mirror attached to the wire. The torsion is balanced in a new position centered around the angle $\alpha_0$ which differs from the initial position. In this position, the sum of all acting torques must be equal to zero. These torques are namely:

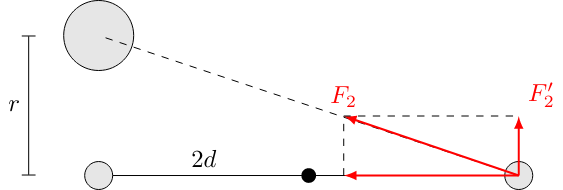
• The torque created by the gravitational attraction of the neighboring large balls: $$M_{1} = 2dF_{1} = 2dG\frac{m_{1}m_{2}}{r^{2}}$$ with $r$ being the distance between the centroids of the balls. The quantity $d$ is defined as the distance between the small balls and the rotation axis. Factor 2 occurs because the attracting force acts on both balls simultaneously.
• The torque created by the gravitational attraction of a small ball and the opposite large balls.
  Forces of large balls acting on small balls at opposite site.
  Te force acting on them is given as $$F_2 = G\frac{m_1m_2}{b^2}$$ with the distance $$\boxed{b=\sqrt{r^2 + 4d^2}}$$ However, only the perpendicular component leads to a torque. Taking the ratio $F_2'/F_2 = r/b$ into account, then the force $F_2'$ can be written as $$F_2' = F_2\frac{r}{b} = G\frac{m_1m_2}{b^2}\frac{r}{b} = F_1\frac{r^3}{b^3}$$ The total torque from both masses can therefore be written as $$M = M_1 - M_2 = 2dG\frac{m_1m_2}{r^2}\beta$$ Here, $\beta$ was used to replace the term $1-r^3/b^3$: $$\boxed{\beta = 1-\frac{r^3}{b^3}}$$
• In the case of equilibrium, the resulting torque is fully compensated by the created torque of the wire given as $$M = D\alpha_0$$ with the proportional constant $D$. Since $D$ is not known, it has to be determined using the oscillation period the wire given as $$T = 2\pi\sqrt{\frac{I}{D}}$$ where $I$ is the momentum of inertia which can be written as $I=2m_1d^2$ for two balls centered around a rotation axis.

Now we can equal both torques and solve the resulting equation for $G$: $$G = \frac{4\pi^2 d r^2 \alpha_0}{T^2m_2\beta}$$ In order to determine $\alpha_0$, the two large balls are brought to the initial position P2. After measuring the position $S_2$ of the laser spot, the position of the large balls is changed to P1, and the position $S_1$ of the spot is measured again. The angle $\alpha$ can then be calculated from from the difference between these positions $S_0 = S_2 - S_1$ according to the following equation: $$4\alpha_0 = \frac{S_0}{L}$$ Here, it has to be taken into account that the angle is twice as large as the rotation angle of the mirror. For the angle $\alpha_0$ it follows $$\alpha_0 = \frac{S_0}{4L}$$ Now we can finally calculate the gravitational constant by inserting all measured and known values: $$\boxed{G = \frac{\pi^2dr^2S_0}{T^2m_2L\beta}}$$ In the given setup, the following parameters are given:

• Mass of small balls: $m_2 = 1.5\,\mathrm{kg}$
• Mass of small balls: $m_1 = 38.3\,\mathrm{g}$
• Distance between balls: $r = 46.5\,\mathrm{mm}$
• Distance between small balls and rotation axis: $d = 50\,\mathrm{mm}$
• Distance between mirror and scale: $(L=464\pm 3)\,\mathrm{cm}$

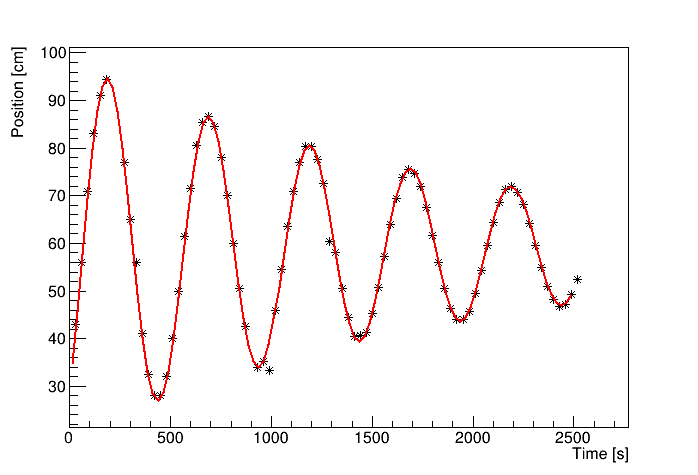
The position of the laser performs a damped oscillation around the position $S_0$. This position and the period time $T$ have to be determined either graphically or analytically with the help of a fit function. For this analysis, the following fit function was used: $$a e^{bx}\sin (cx + d)+e$$ In this function, $a$--$e$ are unknown fit parameters to be determined. The exponential term in front of the sine function is used to take weak damping into account. However, the damping factor $b$ is not used in this analysis. After applying the fit to the data points, the parameter $c$ is determined to be 0.012539. The period has to be calculated with $$T = \frac{2\pi}{c} = 500.23\,\mathrm{s}$$ For parameter $e = 58.7319$ was determined for position P2, and $e = 69.6075$ for position P1. The difference between both is equal to the unknown position $S_0$: $$S_0 = 10.8756\,\mathrm{cm}$$ Inserting all results into the formula for $G$ results in the value $$G = 7.19\cdot 10^{-11}\,\frac{\mathrm{N}\,\mathrm{m}^2}{\mathrm{kg}^2}$$