Franck-Hertz Experiment
Objectives
The following goals should be achieved:
- To demonstrate the concept of quantization of energy levels according to Bohr's model
- To record the Franck-Hertz Curve for mercury
- To measure the discontinuous energy emission of free electrons for inelastic collision
- To interpret the measurement results as representing discrete energy absorption by mercury atoms
Setup
The setup consists of:
- Frank-Hertz tube (Hg)
- Electric oven to heat up the Hg
- Frank-Hertz supply unit
- Temperature sensor
- Two-channel oscilloscope or PC
Theory
James Franck and Gustav Hertz conducted an experiment in 1914, which demonstrated the existence of excited states in mercury atoms. It confirms the prediction of quantum theory that electrons occupy only discrete, quantized energy states. This experiment supports Bohr's model of atoms. For this great invention, they have been awarded Nobel Prize in Physics in the year 1925.
The setup used for the experiment consists of a tube containing low-pressure gas, fitted with three electrodes: a cathode for electron emission, a mesh grid for the acceleration of electrons, and a collecting plate.
With the help of thermionic emission, electrons are emitted by a heated cathode and then accelerated toward a grid that is at a positive potential, relative to the cathode. The collecting plate is at a lower potential and is negative with respect to the mesh grid. If electrons have sufficient energy on reaching the grid, some will pass through the grid, and reach the collecting plate. Electrons that do not have sufficient energy on reaching the grid will be slowed down and will fall back to the grid.
As long as the electron collision is elastic, the electrons will not lose energy on colliding with gas molecules in the tube. As the accelerating potential increases, the current also increases. But as the accelerating potential reaches a particular value, (4.9eV for mercury, 19eV for neon), each electron posses that much potential and now the collision becomes inelastic. As a result, the energy level of electrons bound to the atom is raised. Now the electron almost loses its energy and the measured current drops.
Procedure
- Adjust $U_1= 0.5, 0.7, 1, 1.5\,\mathrm{V}$ and $U_3 = 10\,\mathrm{V}$.
- Record the current versus $U_2$ (0 to 80 V).
- Record the voltage corresponding to each peak
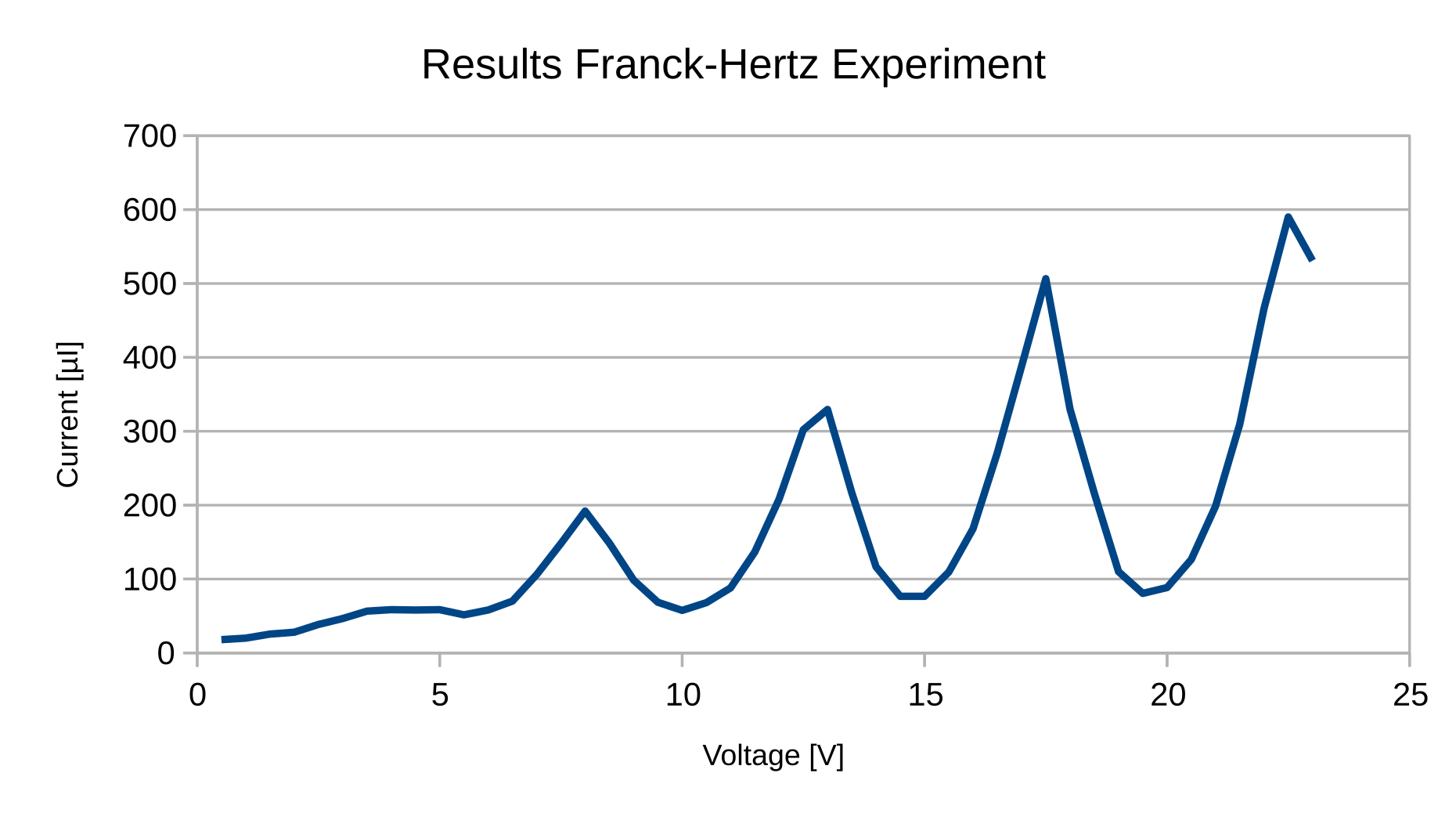
Task
The graph is plotted with the measured data. The average voltage difference for the maxima obtained graphically to
$$\Delta U = 4.625\,\mathrm{V}$$
The difference in the energy levels is therefore
$$\Delta E = eU = 4.625\,\mathrm{eV}$$
Now we can calculate the photon wavelength emitted by the mercury according to
$$\lambda = \frac{hc}{eU} = 268.07\,\mathrm{nm}$$
This value is very close to the literature value of 253.7 nm for that transition.
This page contains 579 words and 3654 characters.
Last modified: 2022-10-01 18:35:37 by mustafa