Boundary Areas

Especially in the interaction between a liquid and a solid phase, the terms adhesion are used for the attraction of the particles between the two phases and cohesion for the attractive forces of the particles in one phase among themselves. Cohesion forces are caused by electrical interactions between the particles and are often also called Van der Waals forces. In the case of polar substances such as water, they can be very pronounced, or, as in the case of non-polar substances, they can be significantly weaker due to induced dipoles. The collisions between the particles cause shifts in the charge centers. If the adhesion is greater than the cohesion, then the liquid spreads out and completely wets the surface. On the other hand, if the cohesion is greater, the liquid is repelled by the surface and a spherical droplet shape is formed. Electrical forces of attraction between particles also play an important role in adhesion. The adhesive forces always depend on the chemical and physical properties of both substances involved.

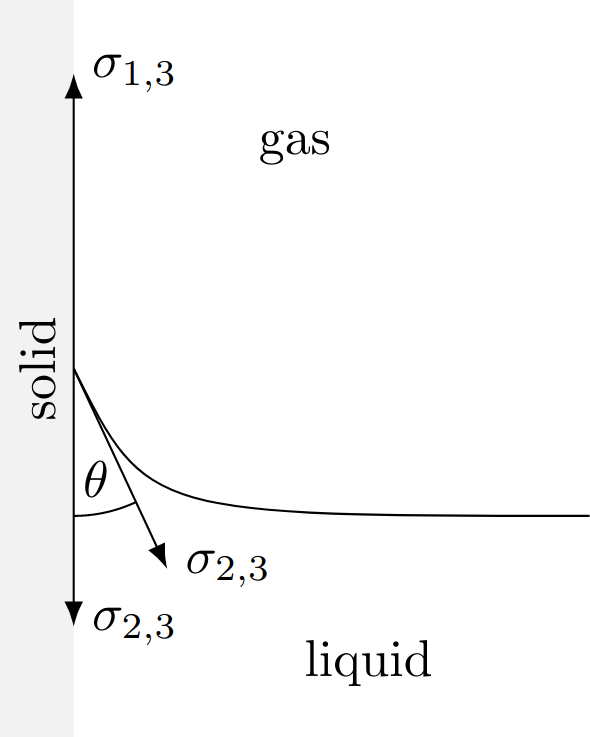
The interaction processes between different substances should now be analyzed in more detail: In addition to the interface between liquids and gases already considered in the last section, we now have to consider the more general case of interfaces between solid (1), liquid (2) and gaseous (3) phases, where for each of these interfaces, analogous to the surface tension, an interfacial tension $\sigma_{i,j}$ is introduced, which is equal to the specific interfacial energy $\varepsilon_{i,j}$. The indices $i$ and $j$ can therefore assume the integer values ​​1 to 3. The quantity $\varepsilon_{2,3} = \sigma_{2,3}$ is therefore the already considered surface tension of any liquid. Just as with water, $\varepsilon_{2,3}$ must always be positive so that it remains stable, otherwise, the particles would pass into the gaseous phase. The interfacial energy $\varepsilon_{1,2}$ is directly related to the adhesion forces between the liquid and the solid. The also existing interactions between the gaseous and solid phase are described with $\varepsilon_{1,3}$. The three forces resulting from the interfacial tensions $\sigma_{i,j}$ also act tangentially to the boundary layers, which leads to a deformation that is not noticeable in the case of the solid phase. The surface of the liquid, on the other hand, changes in such a way that the resulting force at the point of contact of all three phases disappears.

A projection of $\sigma_{2,3}$ onto the interfacial tensions tangential to the solid phase results in the \textit{Young's equation}\index{Young's equation} named after Thomas Young: $$\boxed{\sigma_{1,2} + \sigma_{2,3}\cos\varphi - \sigma_{1,3} = 0}$$ or changed to $\cos\varphi$: $$\cos{\varphi } = \frac{\sigma _{1,3} - \sigma _{1,2}}{\sigma _{2,3}}$$ If $\sigma_{1,3}$ is larger than $\sigma_{1,2}$, then $\cos\varphi > 0$ and thus $\varphi < 90^\circ$. The liquid then forms a concavely curved surface and is therefore wetting. This applies, for example, to water in a glass container. In this case, the resulting angle is almost exactly $\varphi = 20^\circ$. Because of its shape, this bulge is also known as a meniscus (Greek for crescent). When reading the scale in a container provided for this purpose, care must be taken to always use the underside of the bulge, otherwise, the volume will be determined incorrectly. Conversely, $\sigma_{1,3} < \sigma_{1,2}$ is $\varphi > 90^\circ$, resulting in a convex curved surface. An example of this is a glass vessel filled with mercury since the enlargement of the solid -- gaseous boundary layer is energetically more favorable here.

If you put a thin tube (capillaries) with the inner radius $r$ into a liquid, then the liquid inside rises to the height $h$ above the liquid level outside due to the interfacial tension. This behavior is commonly referred to as capillarity. This increases the potential energy according to: $$\Delta E_\mathrm{pot} = mgh = V\varrho g \Delta h$$ With $V=\pi r^2 h$ for a cylinder volume, this results in $$\Delta E_\mathrm{pot} = \pi r^2 \varrho g h \Delta h$$ At the same time, the surface energy changes according to the surface of a cylinder $A = 2\pi r h$: $$\Delta E_\mathrm{O} = - (\sigma_{1,3} - \sigma_{1,2}) 2 \pi r\Delta h$$ Using the previously derived equation and he fact that $\sigma_{2,3}$ equals the surface tension $\sigma$ results in: $$\Delta E_\mathrm{O} = 2\pi r \sigma \cos{\varphi } \Delta h$$ A constant height is set for the condition $\Delta E_\mathrm{pot} = -\Delta E_\mathrm{O}$. Inserting the two equations then leads to the following formula for calculating $h$: $$\boxed{h = \frac{2\sigma\cos\varphi}{rg\varrho}}$$ The surface tension of a liquid can thus be measured in a simple manner by determining the height and the contact angle.