Carnot Process

• The Carnot process is a cyclic process designed as a thought experiment.
• The process contains 2 isothermic and 2 adiabatic transitions.
• It leads to the highest efficienciies in converting heat energy into mechanical motion with heat engines and the highest coefficient of performance for chillers.
• The efficiency $\eta$ and the coefficient of performance $\varepsilon$ are derived to $$\eta = \frac{T_1 - T_2}{T_1}\qquad \varepsilon = \frac{T_1}{T_1 - T_2}$$

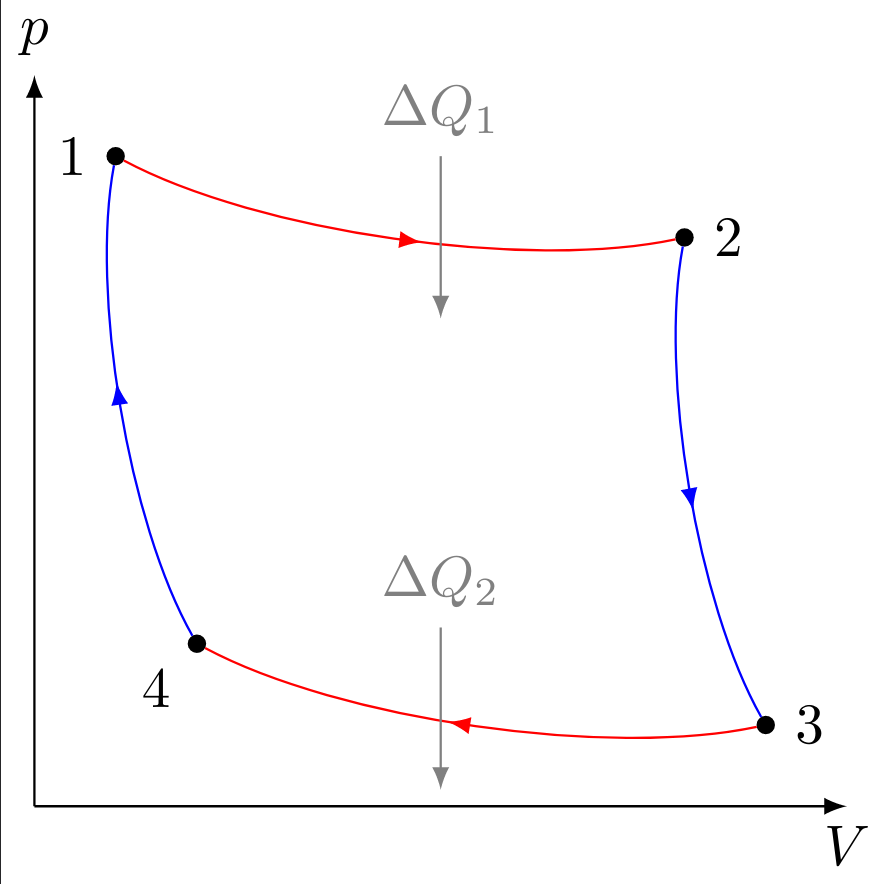
A heat engine such as a steam engine or car engine converts thermal energy into mechanical work. After running through a cyclic process, the machine returns to its initial state and thus works periodically. If it is possible to let the cyclic process run in the opposite direction, it is called reversible. Otherwise, it is called irreversible. A simple example of considering the thermodynamic laws is the Carnot cycle process named after Nicolas Léonard Sadi Carnot. The main idea behind it will be explained in the following: We start at an arbitrarily chosen point 1 at the top left of a $p$-$V$ diagram with pressure on the $y$ axis and volume on the $x$ axis. Furthermore, for the sake of simplicity, we use an ideal gas in our thought experiment, so that all calculations can be carried out analytically. First, the gas is expanded isothermally until point 2 is reached. To do this, the thermal energy $\Delta Q_1$ must be supplied from outside. Because the temperature and thus the internal energy of the gas is constant, the first law of thermodynamics applies $$\mathrm{d}Q = p\,\mathrm{d} V$$ The added thermal energy is thus completely converted into mechanical work: $$\Delta W_{1,2} = \int_{V_1}^{V_2} p\,\mathrm{d} V$$ In the following, we consider only an amount of substance of 1 mol and can thus calculate the mechanical energy directly using the ideal gas equation: $$\Delta W = \int_{V_1}^{V_2}\frac{RT_1}{V}\,\mathrm{d} V = RT_1\ln\left(\frac{V_2}{V_1}\right)$$ After that, an adiabatic expansion leads to point 3. Here the change in the amount of heat is $\mathrm{d} Q = 0$, and for the mechanical work applies $$\Delta W_{2,3} = \mathrm{d} U = -p\,\mathrm{d} V$$ From here the gas is isothermally compressed to point 4. To do this, the heat energy $\Delta Q_2$ must be withdrawn from the system, so that the work on the system $$\Delta W_{3,4} = RT_2\ln\left(\frac{V_3}{V_4}\right)$$ must be done. Finally, the gas is again adiabatically compressed and the process starts again after reaching point 1. Since the work done on the system during adiabatic compression is equal to the work done by the system during adiabatic expansion, both amounts cancel each other out in the overall balance. In the net balance, therefore, only the work in the isothermal steps has to be taken into account: $$\Delta W = \Delta W_{1,2} + \Delta W_{3,4}$$ This leads to $$\Delta W = RT_1\ln\left(\frac{V_2}{V_1}\right) + RT_2\ln\left(\frac{V_3}{V_4}\right)$$ The following two conditions result from the adiabatic equation: $$T_1V^{\kappa-1}_2 = T_2V_3^{\kappa-1}$$ $$T_1V^{\kappa-1}_1 = T_2V_4^{\kappa-1}$$ Dividing the first by the second equation gives: $$\frac{V_2}{V_1} = \frac{V_3}{V_4}$$ The total work done by the two isothermal processes is then given by: $$\Delta W = R(T_1 - T_2)\ln\left(\frac{V_1}{V_2}\right)$$ The heat given off can no longer be used. It therefore makes sense to define the efficiency $\eta$ of such a heat engine from the ratio of work done to heat absorbed: $$\eta = \left|\frac{\Delta W}{\Delta Q}\right| = \frac{R(T_1-T_2)\ln\left(\frac{V_2}{V_1}\right)}{RT_1\ln\left(\frac{V_2}{V_1}\right)}$$ After simplifying this fraction, the following term remains: $$\boxed{\eta = \frac{T_1 - T_2}{T_1}}$$ The efficiency, therefore, depends only on the temperature difference between the two heat reservoirs between which the system transports the heat back and forth. If you operate a Carnot machine in the opposite direction, you get a so-called chiller, which transports heat from a colder to a warmer reservoir. Typical examples of such a chiller are heat pumps or refrigerators. Instead of the efficiency, the coefficient of performance (COP) is given as the ratio $$\varepsilon = \frac{\Delta Q_1}{\Delta W}$$ is defined by the amount of heat released $\Delta Q_1$ and the work put into the system $\Delta W$, which corresponds exactly to the inverse efficiency: $$\boxed{\varepsilon = \frac{T_1}{T_1 - T_2}}$$ If one neglects the two adiabatic processes in the Carnot cycle, which do not contribute to the mechanical work, then only the isothermal compression and expansion remain. This is the best possible conversion of heat into mechanical energy. There can therefore be no thermodynamic machine that converts heat into work with an efficiency better than the Carnot efficiency. At the same time, there cannot be a refrigeration machine whose COP is better than that of a Carnot machine running in reverse. Because the efficiency of a heat engine is always less than 1 and heat can never be completely converted into mechanical energy or into electrical energy by driving a turbine, thermal energy is also referred to as inferior energy. The conversion of high-quality electrical energy into heat, on the other hand, can be carried out with an efficiency of 1. The reason for this is that the movement of particles in a substance is statistically distributed in all directions, while electrical energy, caused by the flow of electrons in a cable, or mechanical energy from the movement of a piston, is always directed.