Gas Laws
Law of Boyle-Mariotte
The first law deals with the relationship between the pressure and the volume of an ideal gas. Robert Boyle and Edme Mariotte independently found this connection. To find this law, we imagine that the ideal gas is in a vessel that is hermetically sealed with a moving piston. The piston is weighed down with weights so that a defined pressure is created in the gas, which can be calculated from the weight and the cross-sectional area of the piston. It is important for the investigation that the temperature is kept constant the whole time. This is called an
isothermic process. In addition, the container must be tight enough to prevent an exchange of particles with the environment can take place, otherwise, this is no longer a closed system.
If you increase the number of weights and thus push the piston further into the vessel, you will first notice an increase in temperature. The measurement can therefore only be carried out when the temperature has dropped to room temperature. The results are typically plotted within a $p$-$V$ diagram with the pressure on the $y$-axis and the volume on the $x$-axis. As an example, a gas volume of $10\,\mathrm{cm}^3$ under normal conditions was chosen, i.e. a pressure of around 1 bar and a temperature of 20°C. Precisre measurements have shown that the height of the piston and thus the volume itself decreases in proportion to the pressure, i.e. it applies
$$V \propto \frac{1}{p}$$
In other words: the product of pressure and volume is always constant for an ideal gas:
$$\boxed{pV = \mathrm{const}}$$
This experimental result is very interesting since we already linked the product $pV$ to the mechanical energy. If $pV$ is constant whenever $T$ is constant, we can predict that the energy of a gas must be connected to the temperature which we will discuss in the section on kinetic gas theory a bit deeper. Another way to write down the derived law is as follows:
$$\boxed{p_1 V_1 = p_2 V_2}$$
All three notations are equivalent to each other and are used in the literature to represent Boyle-Mariotte's law.
Law of Guy Lussac
A similar law was discovered by Jacques Charles and Joseph Louis Gay-Lussac for a relationship between volume and temperature.
If one changes the previous setup in such a way that one can increase the temperature of the gas by adding heat, then a proportionality between volume and temperature can be established if the number of weights and thus the ram pressure is kept constant. There is thus an
isobaric process. Accordingly, Gay-Lussac's law can be interpreted analogously to Boyle-Marriott as
$$\boxed{\frac{V}{T} = \mathrm{const}}$$
The temperature must of course be used in Kelvin in order to obtain meaningful results.
Law of Amontons
Amontons law deals with the last combination of the three states. This is a
isochoric state change. This means that the volume remains constant, but the temperature and pressure change. Guillaume Amontons found that both quantities are proportional to each other, so one can write:
$$\boxed{\frac{p}{T} = \mathrm{const}}$$
This page contains 660 words and 3897 characters.
Last modified: 2022-10-01 20:34:21 by mustafa
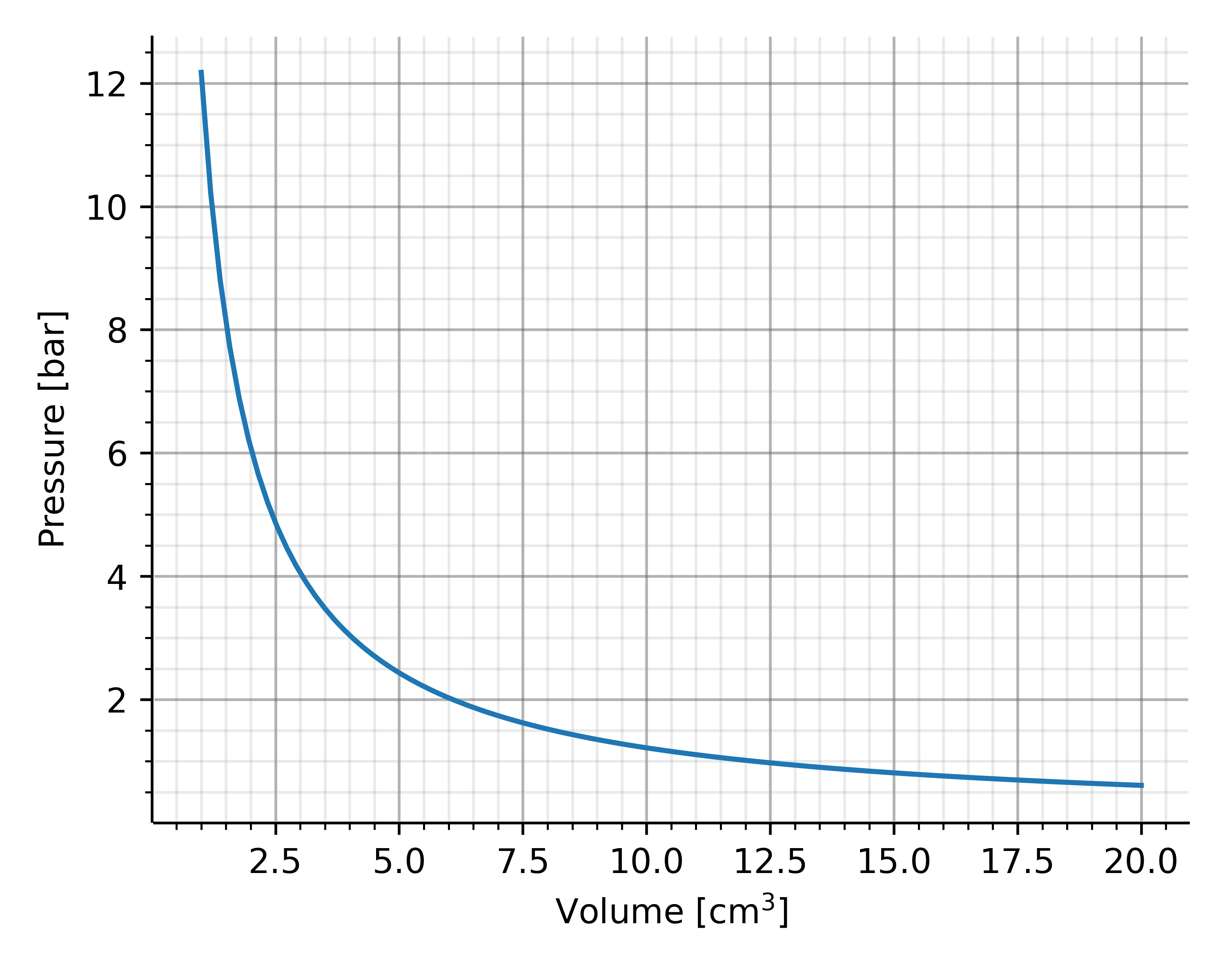 Possible outcome for measuring the volume of a gas inside a closed vessel when changing the pressure of a moving piston.
Possible outcome for measuring the volume of a gas inside a closed vessel when changing the pressure of a moving piston.

